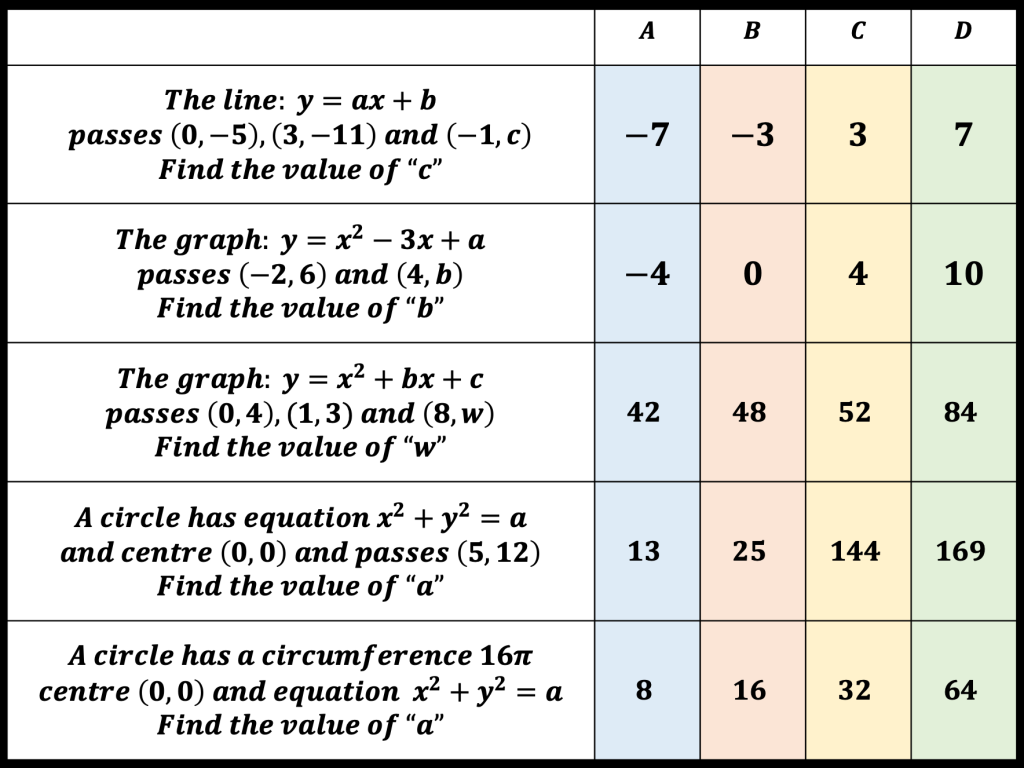
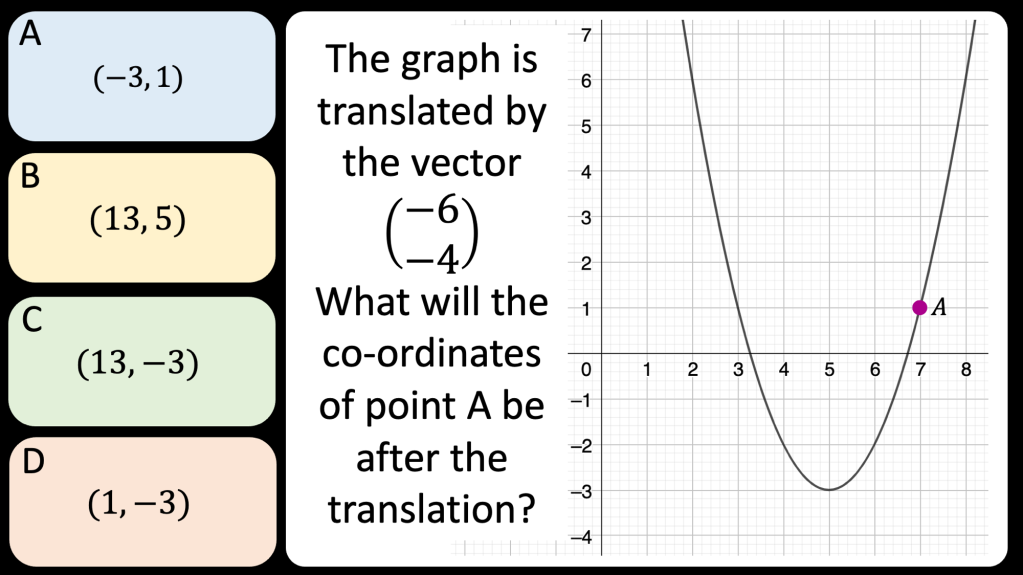
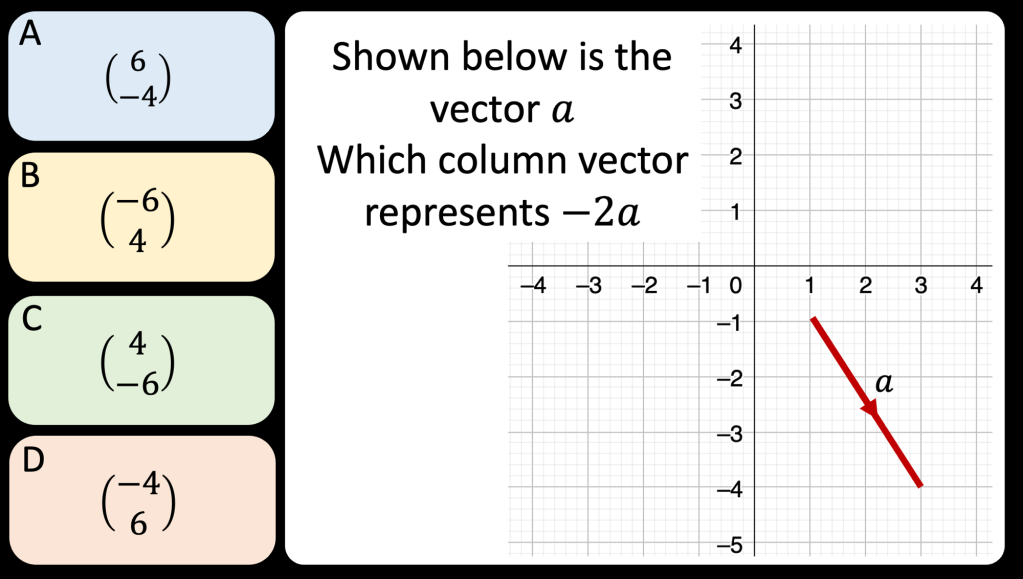
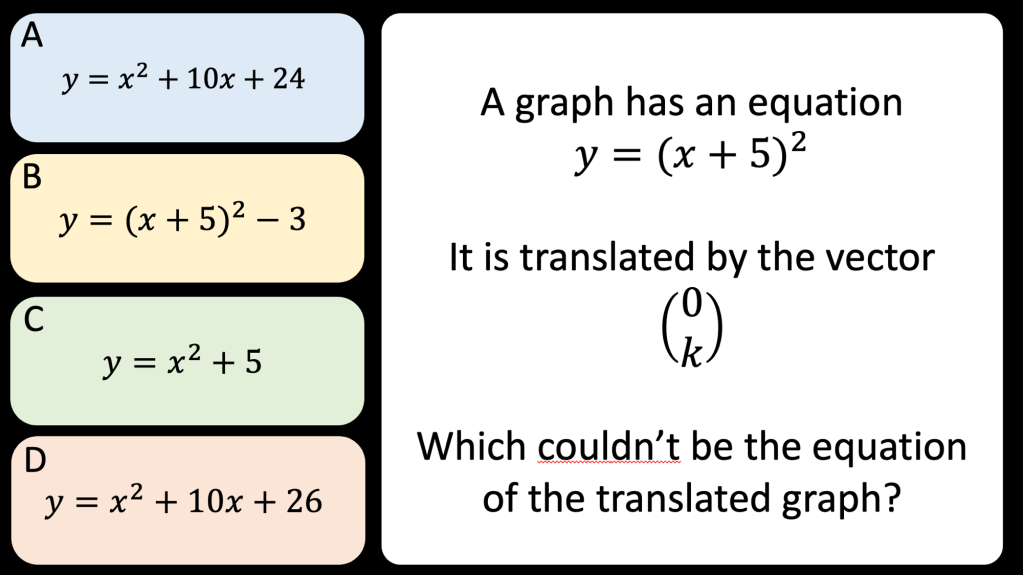
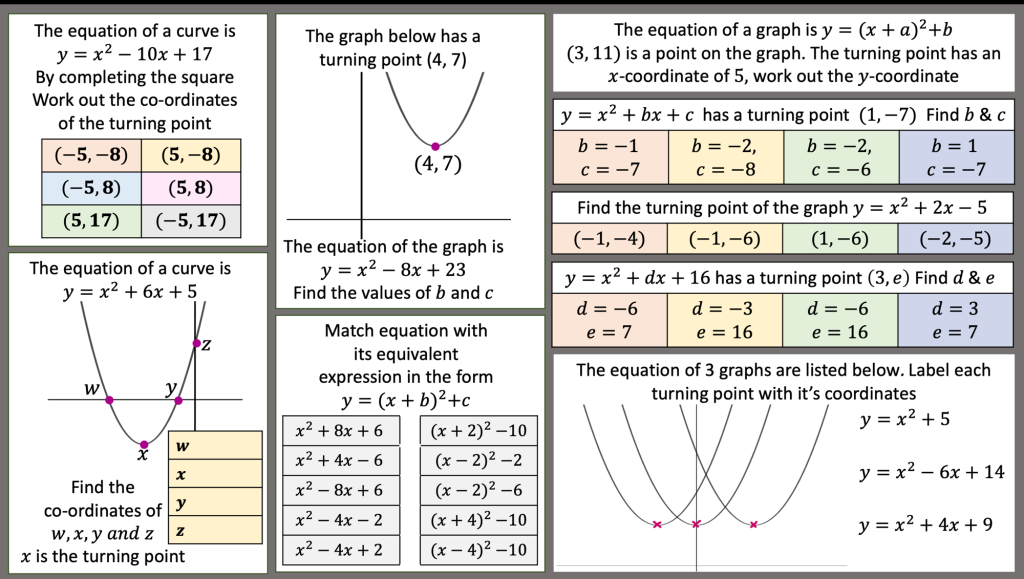
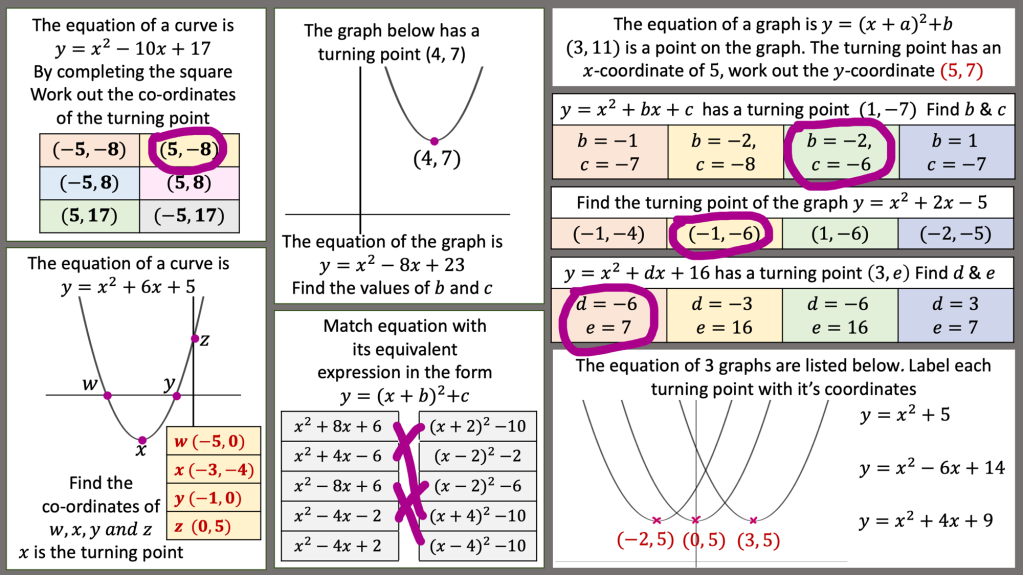
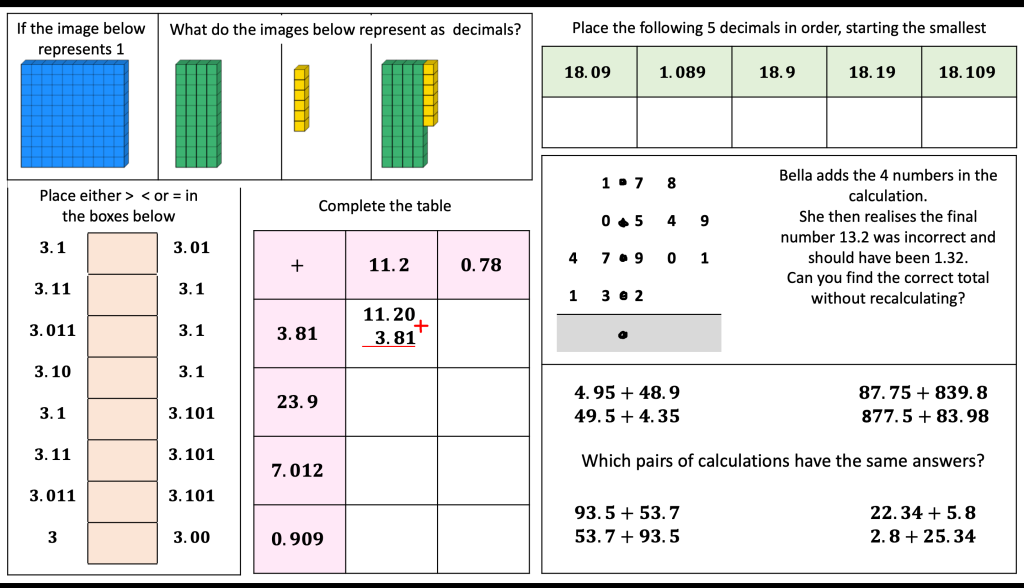
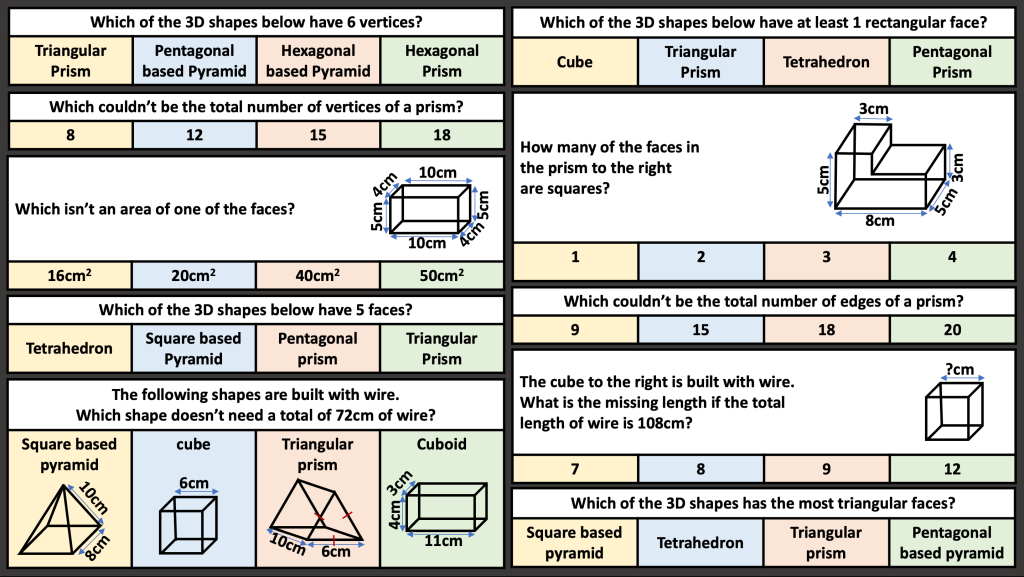
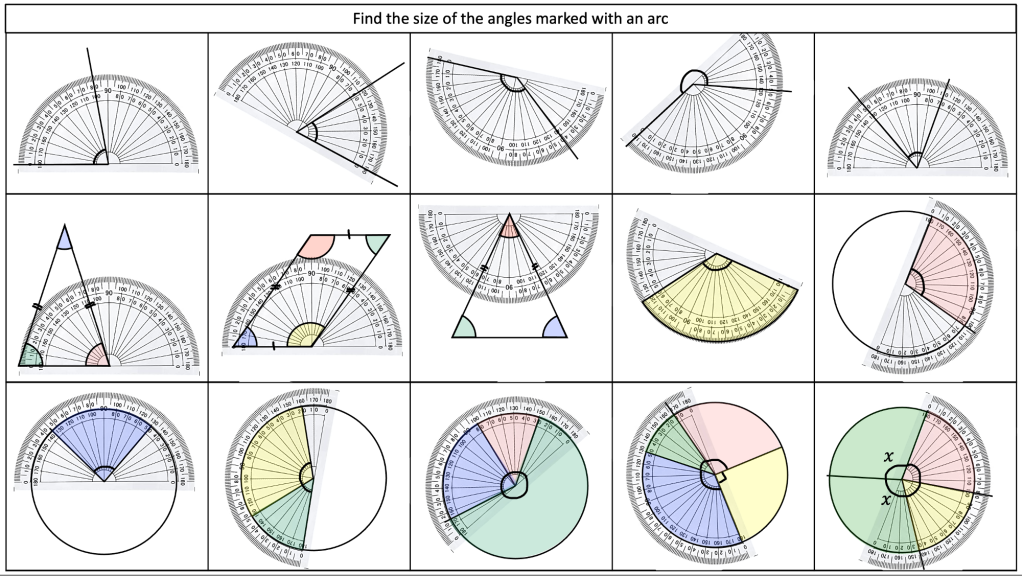
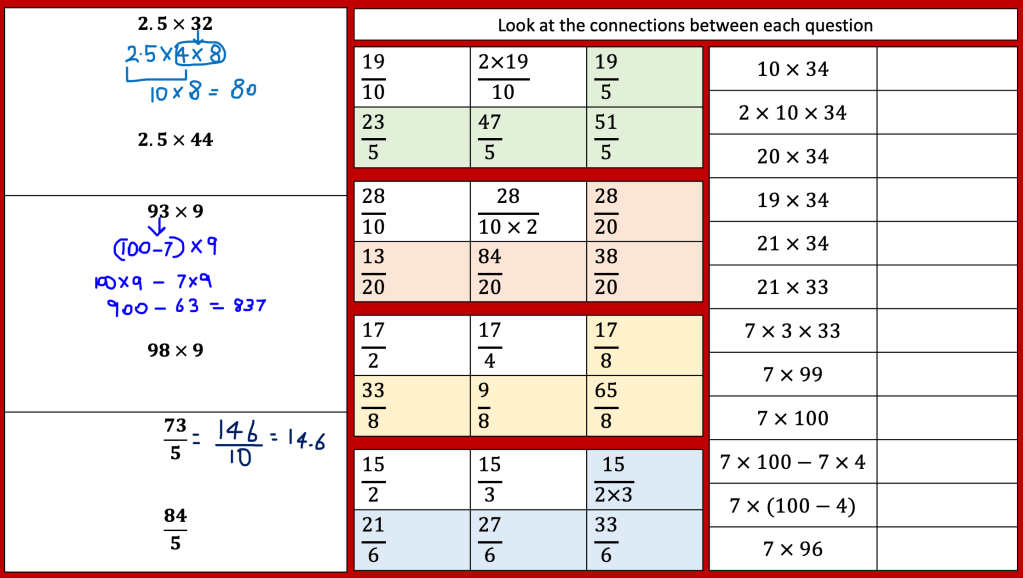
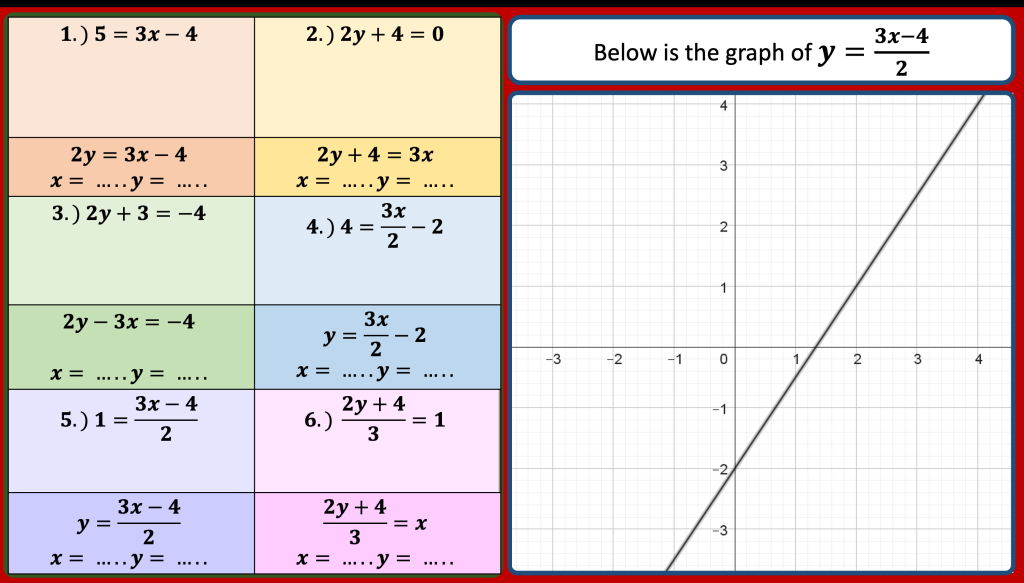
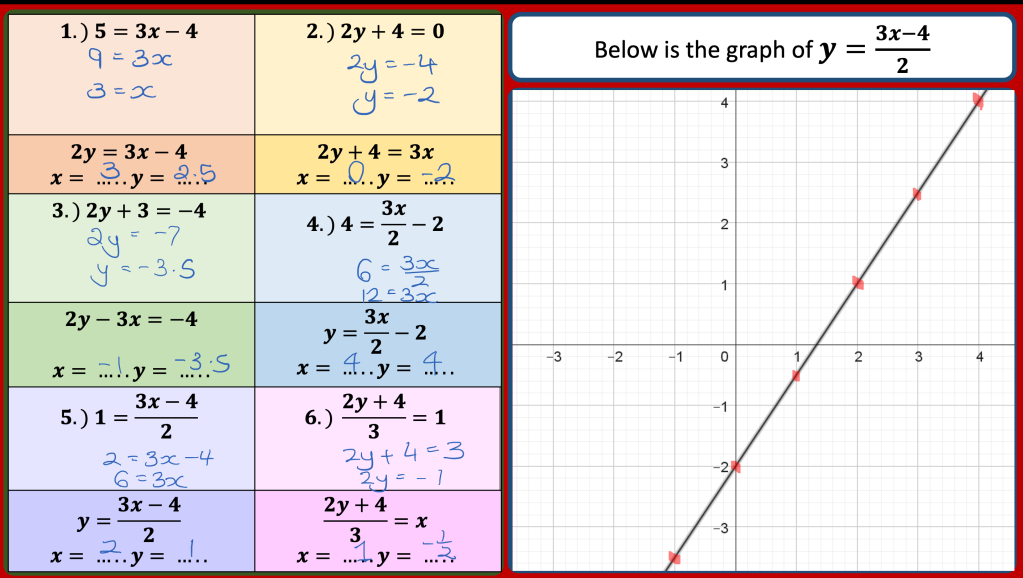
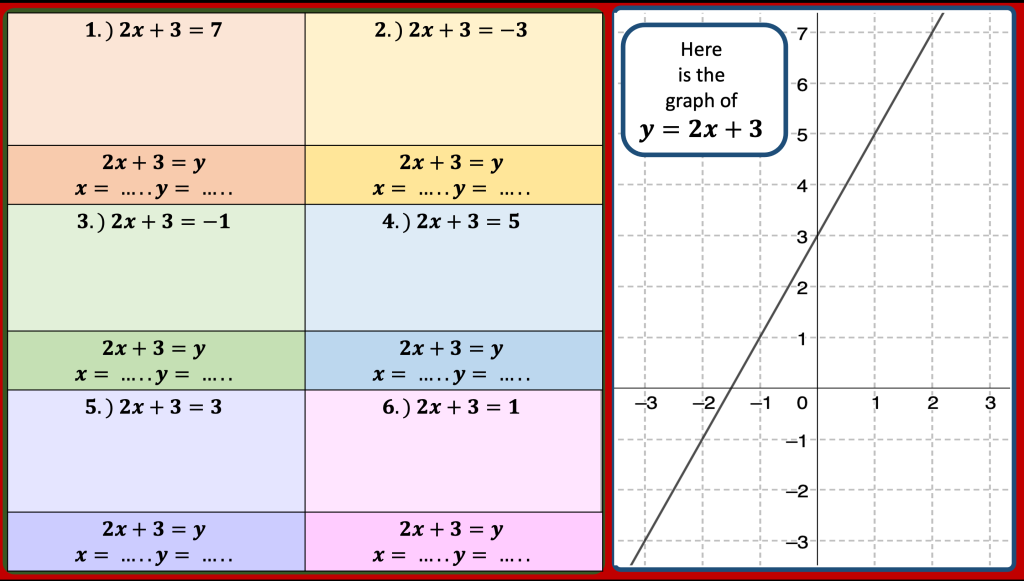
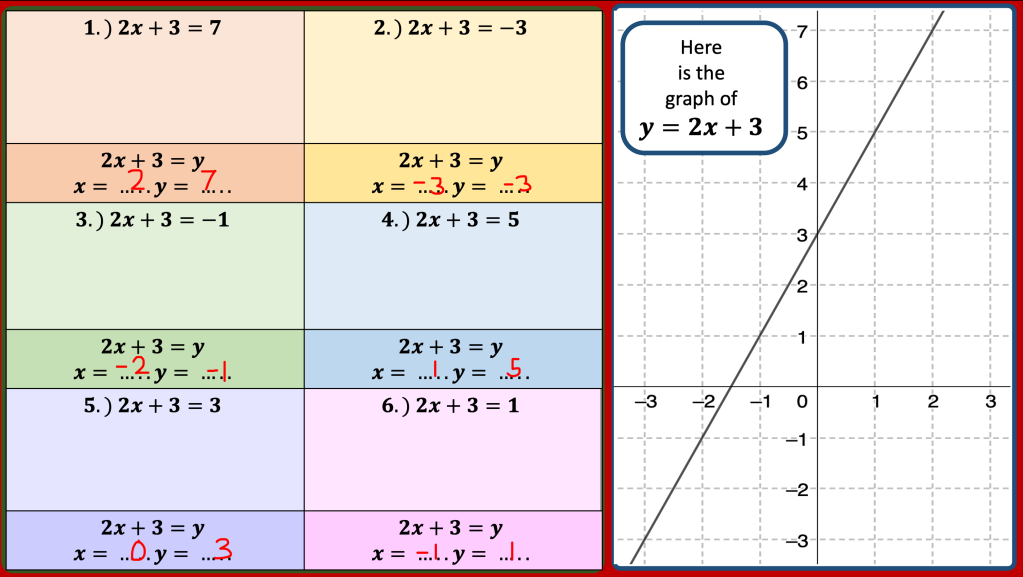
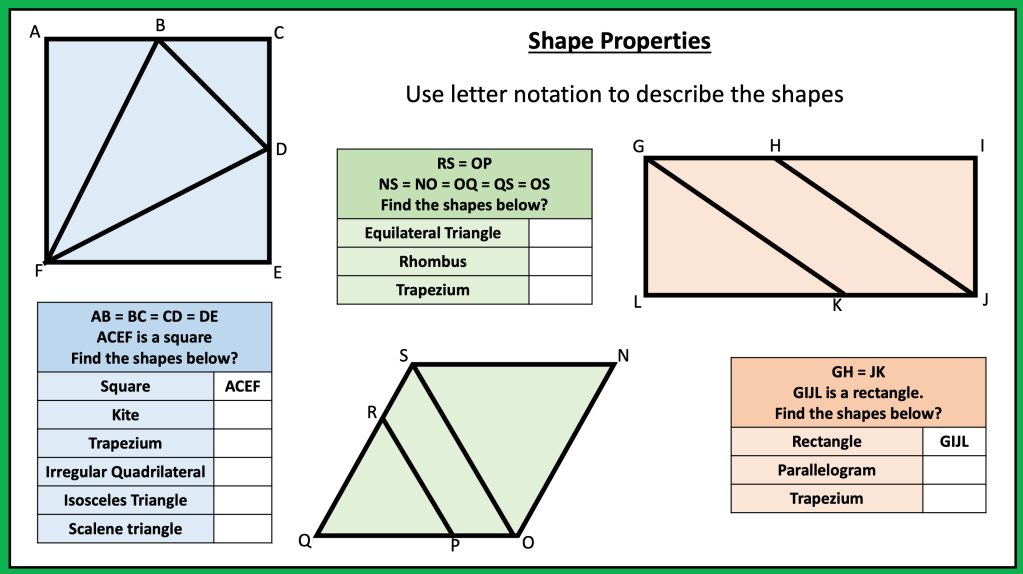
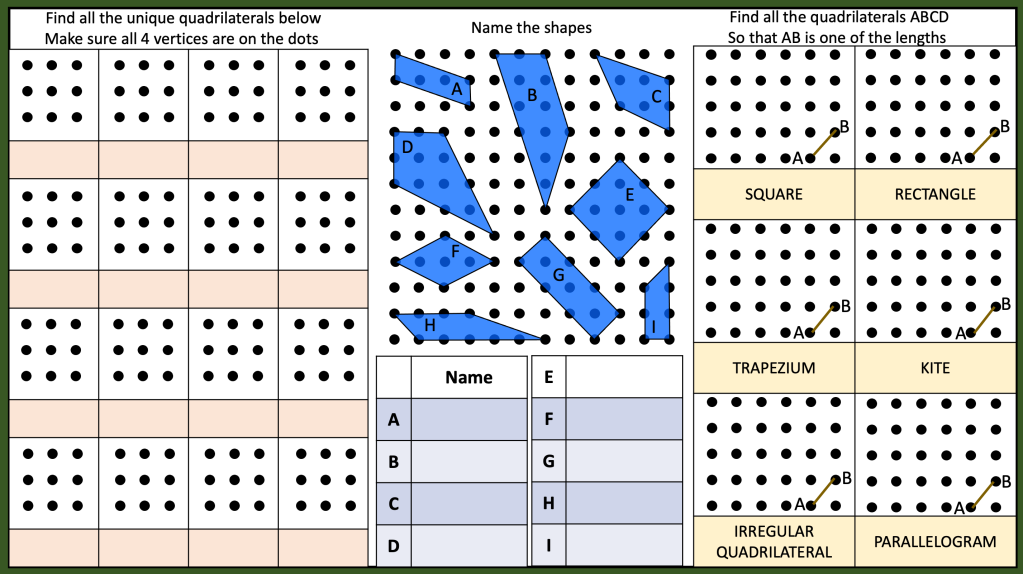
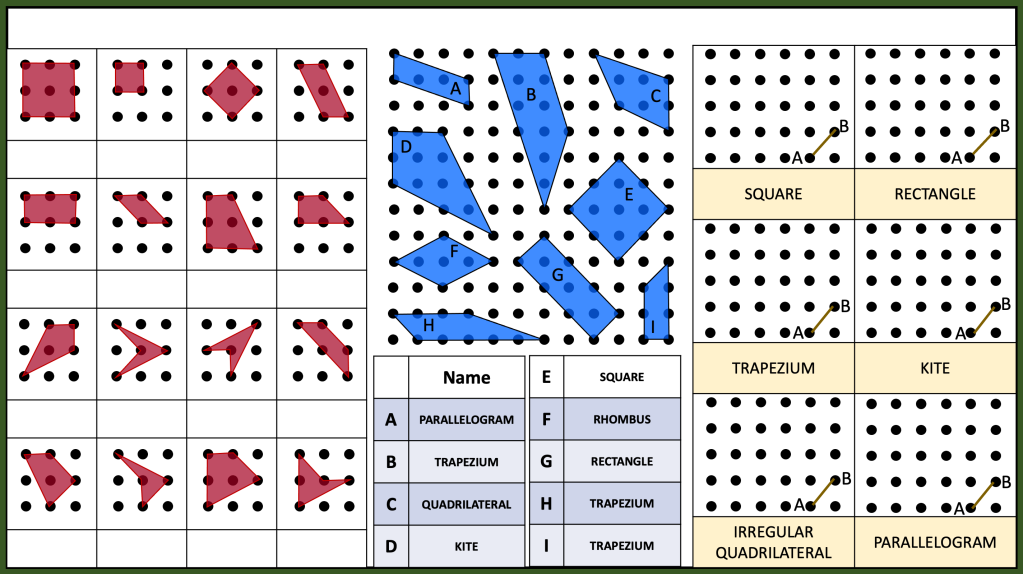
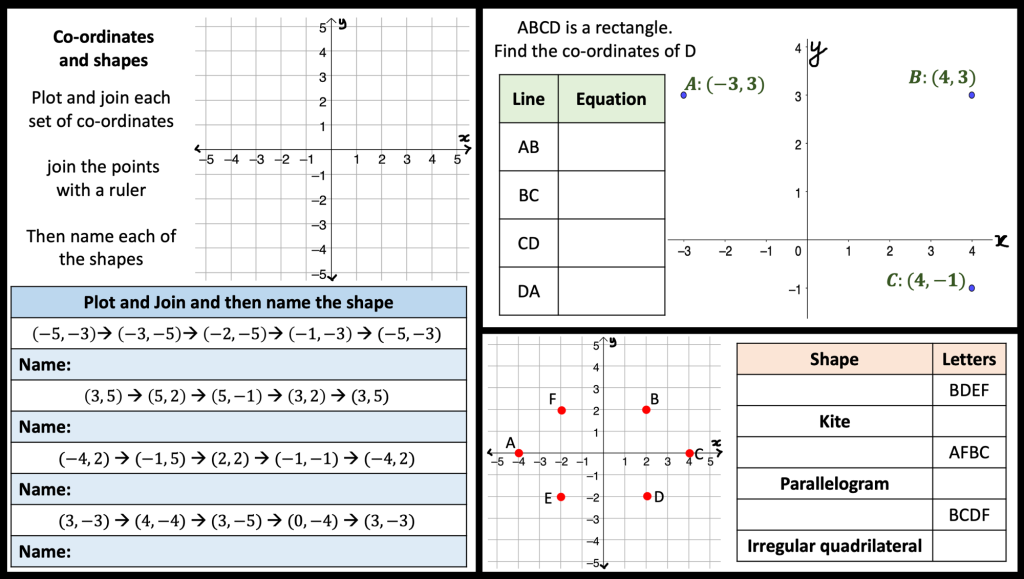
I am reviewing graph transformations and some tasks can be seen in my post on non linear graphs but I am reviewing this topic with year 11 post mocks. I have some vector related MCQs and some McQs on finding missing coefficients in linear and quadratic graphs too.