We are teaching mixed attainment year 7 for the entire year (we used to teach for a half term and then set them) Its been an interesting experience. I have felt more settled because I know my class wont be swapped part way through a year and have to learn new routines and expectations. I also have to keep reminding myself that there will be pupils in the class who might struggle and because I have 24 pupils and not 8, I have to keep reminding myself that this isn’t a set 2 or 3 but a mixed attainment group. Things I have learnt so far:

Students who have prior attainment that would lead you to believe they would struggle have really excelled.

Students who have prior attainment that would lead you to believe that they can work at a faster pace have tried to prove they have the understanding but when given some questions to test their understanding they have struggled.

My first topic was Shape… Area, Perimeter, Volume and Surface Area. These were taught over many lessons but I’ve written about them below like it was a continuous lesson.

I started with discussing Perimeter and how we could measure the distance moved by the robot around a grid. They then discussed what they noticed. Everyone coped well with finding the perimeter and they discussed why the perimeters were equal.

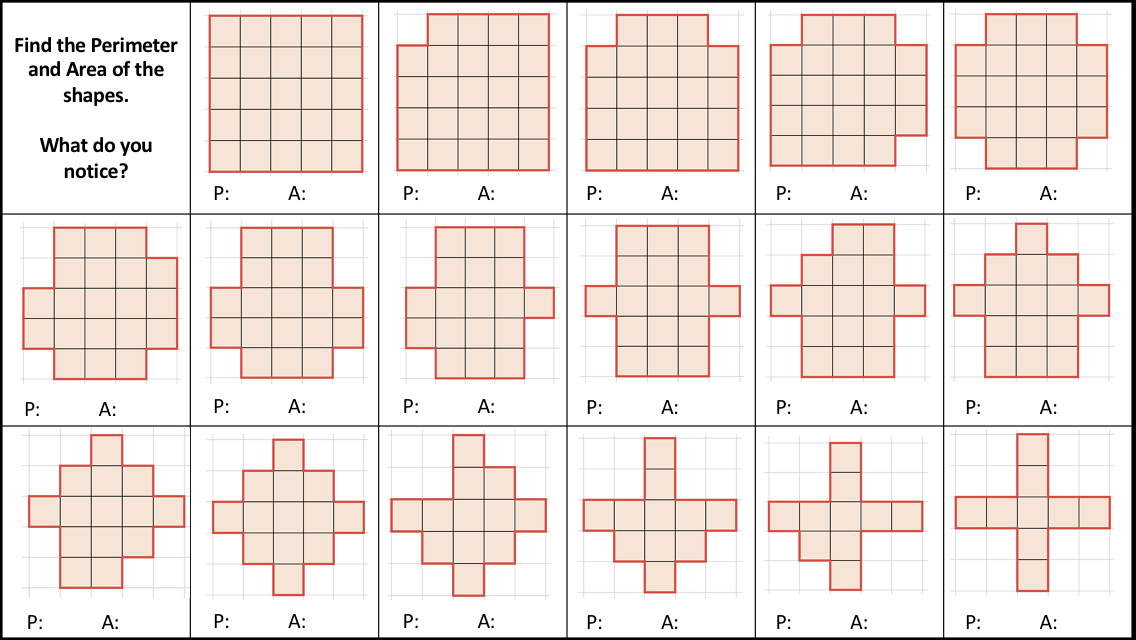
I didn’t want to have tiered questioning but rather have questions that all students could access but form a discussion point about how they answered the questions. I hoped to ask questions that could be answered in a variety of ways but students would learn from each other. Generally this has been the case. Students could all find the perimeter and area of the shapes above but some started to notice links and patterns and set about proving why they were linked.

After Perimeter we looked at Area over several lessons. We started with area of a Rectangles and compound shapes and then looked at Triangles, then looked Kites and Prallelograms, and finished with Trapezium. After spending a lesson looking at Area of Rectangles we looked at compound Area. We use the same question but split in different ways.

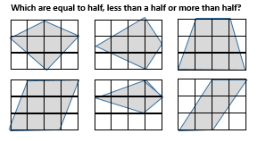
When we looked at triangles we spent some time discussing the fraction shaded in each diagrams. Students came up to the front of the class and showed how they got a quarter in each image.

After looking at the fractions of the images above we looked at the ones below. Students identified that areas and how they were able to find them using half of the rectangle or by moving shapes around.

Then after the area of the triangle we looked at other 2D shapes in this manner.

We were able to find the area of 2D shapes from the area of a rectangle and some students expressed this as a formula and some as a fraction of a rectangle. When we looked at the Trapezium we looked at moving pieces so it formed a rectangle. We discovered that the rectangle formed, always had a length that was the midpoint of the two parallel sides. Some students knew the formula for the area of the trapezium but liked to see how it was derived. Students came to the board to calculate questions and it was nice to see their interpretation of how to find the area.

After we had spent time on the 2D shapes we moved to 3D and looked at Volume. Students used centimetre cubes to find the volume of prisms. We shared answers and discussed multiple methods. We discovered that cuboids had 3 different approaches. you could find the number of cubes from any one of its 3 unique cross-sections and then count the ‘layers’ of the cross-section. This helped the move to cuboids-without-cubes-to-count a lot easier. Students were keen to show me that they could still find the volume in several ways but sometimes there was an ‘easier’ way. EG: Find 25 times 4 then times 7  rather than finding 7 times 25 first.

We then had a lesson that I knew was going to be shortened so we used sticks and had a go at building 3D shapes – in particular prisms. I thought that we could use this to see the number of faces and see the cross section of the prisms we built. The next step is Surface Area and I’m looking forward to looking at nets of prisms.