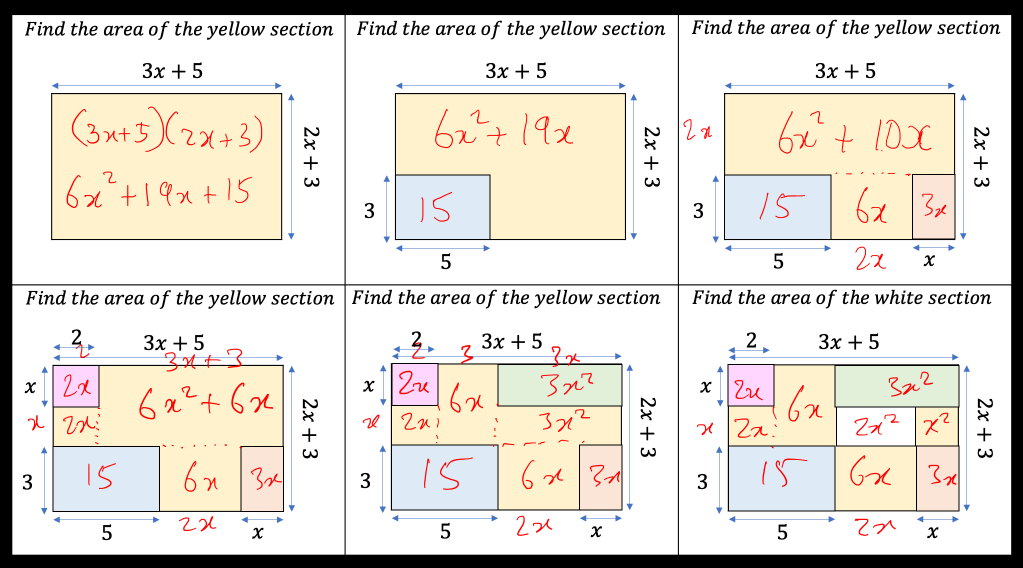
I have been teaching Recurring and Terminating Decimals to year 9 this week and last week. I started off with the task below at the end of this post and it was written several years ago but is still a useful task. The second lesson was when I wanted students to be able to convert a recurring decimal into a fraction. I started off with 0.4 recurring, 0.5 recurring etc. The students could quickly see that these all had a denominator of 9 and when two values recurred, they saw the denominator was 99. I proved this and everyone was happy, but then I showed them a question where some of the numbers terminated and then it recurred. They struggled with this and didn’t notice the pattern i’d hoped they’d see in the sheet below: I hoped they would see that 0.1 recurring was ten times bigger than 0.01recurring so 1/9 could be divided by 10 and so 0.01recurring was equal to 1/90. So I realised we needed to spend longer on this in the next lesson.

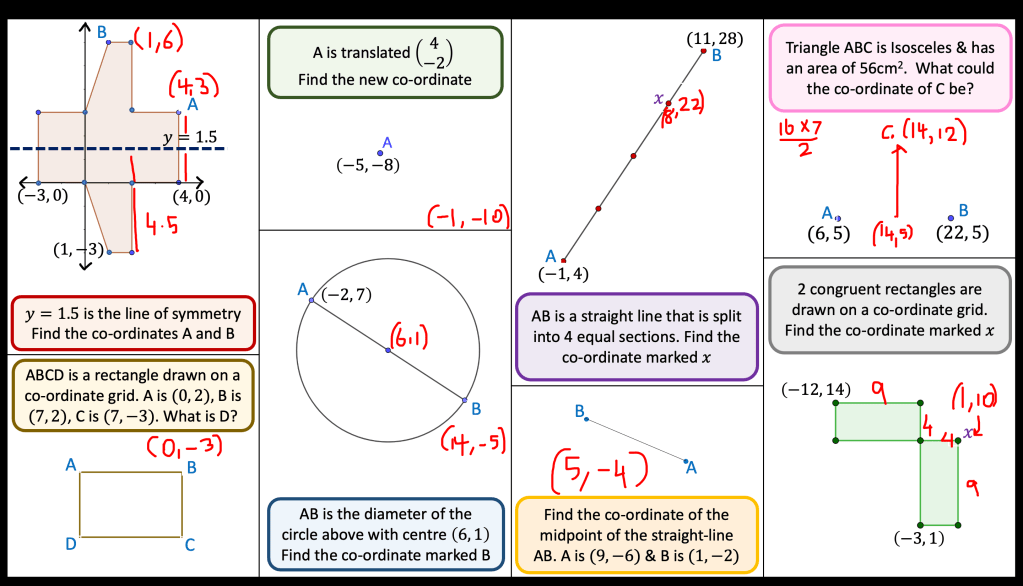
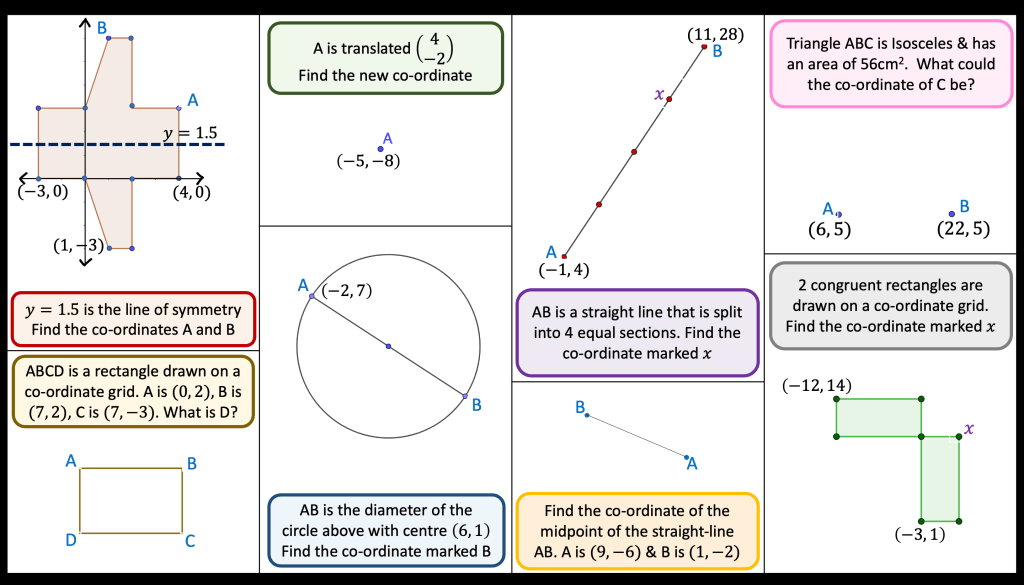
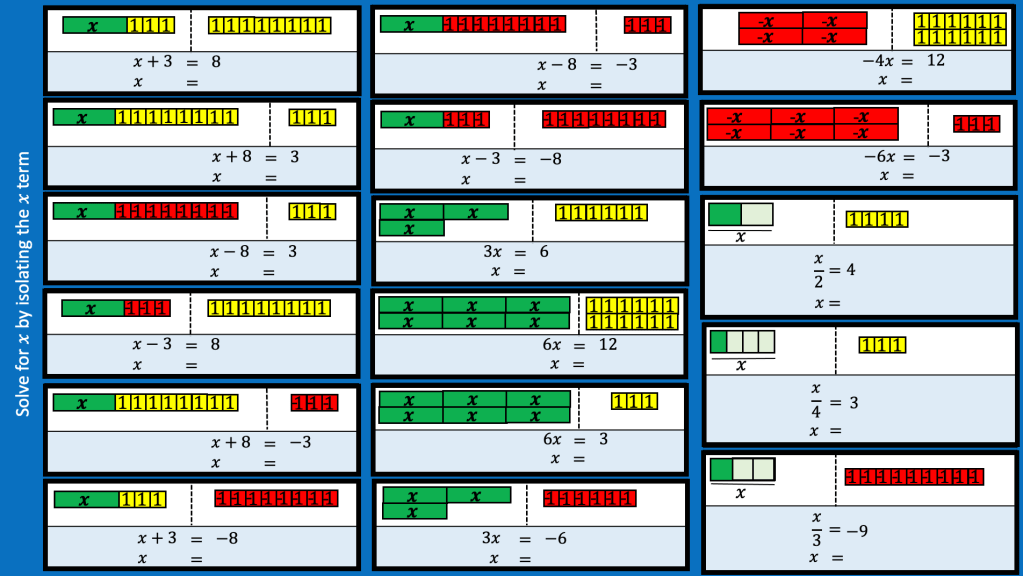
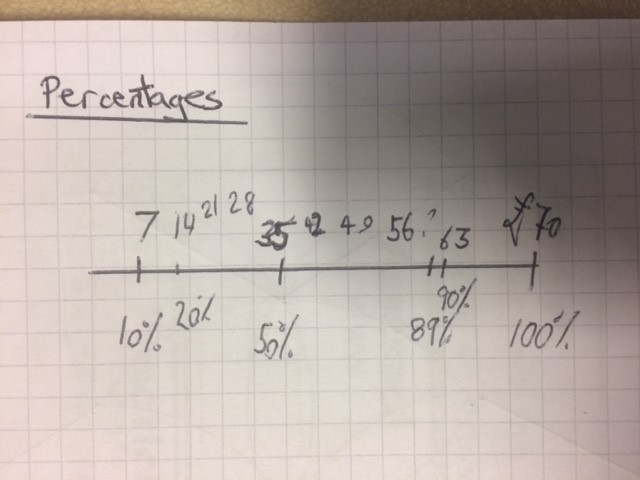
The plan for the next lesson is to start with the slide below as a recap of the previous lesson. The questions are connected so I would like to spend some time discussing how they are related.

Then I want to look at the problem below and usually I would look at the approach in the middle but I am unsure if its worth looking at the blue method. I guess what is worrying me is that the class aren’t as fluent with fractions as I’d hoped so they would struggle to see the connections. I think I will teach the middle method and then see if they can understand what is happening at each stage in the other methods. 
 Recurring Deicmals
Recurring Deicmals
Written in 2017:
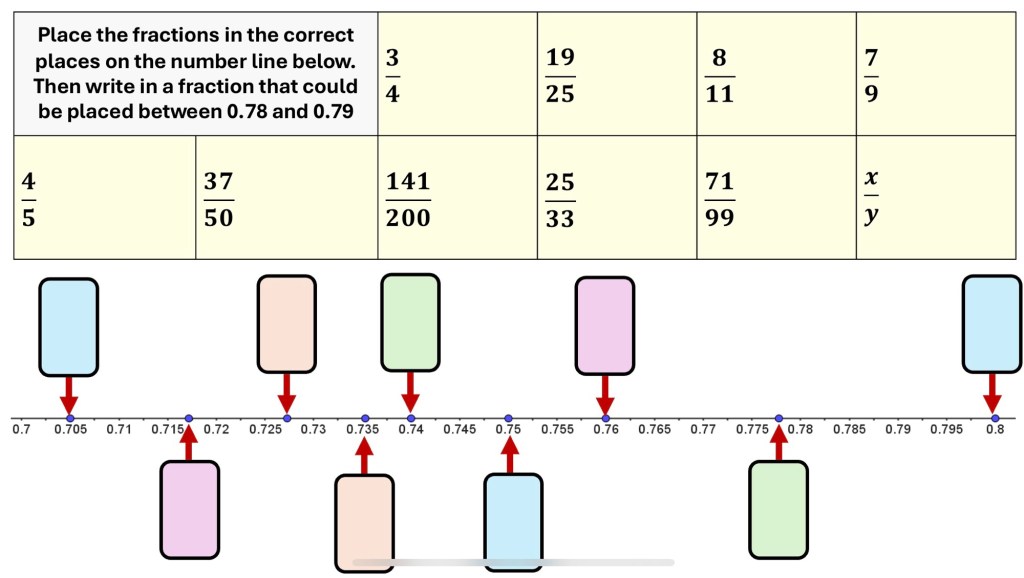
I made this task because i thought students would enjoy trying to find a way of fitting the fractions into the table. I initially came up with the tables and had an idea that i would ask students to find fractions that fit, but then I thought they might just add in easy fractions they knew such as 1/3 and 1/2 but in hindsight i don’t think they would have been as quick to find the fractions and it might have been a better challenge for them to try and find the fractions themselves.

I then gave them a range of fractions that needed to be placed in the table, this might work better with some groups.

but i think with a group that relish a challenge i wouldn’t supply the fractions, or maybe you could give the option of trying to find fractions that fit the table and put up the fractions above if they get stuck. Its important that students know they are finding fractions that equal decimals that fill the criteria
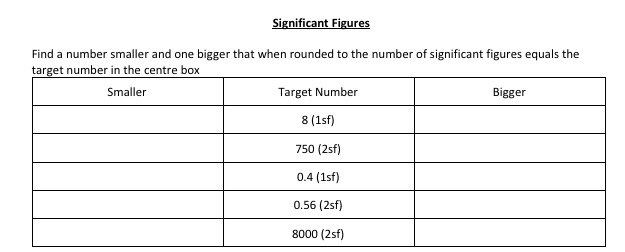
Terminating and Recurring Decimals















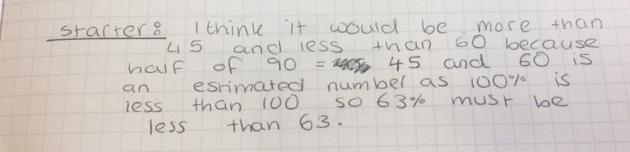

 Update
Update