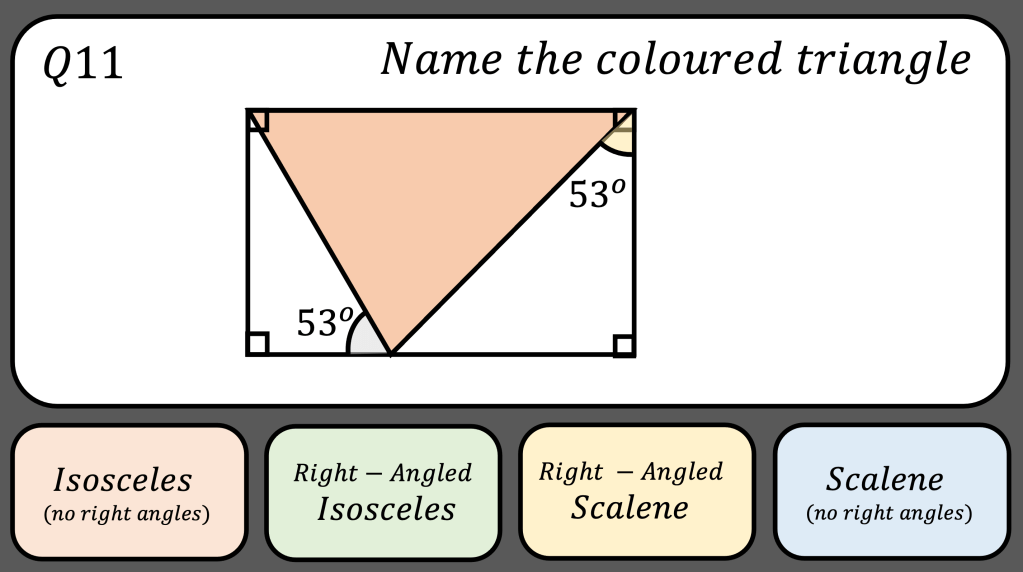
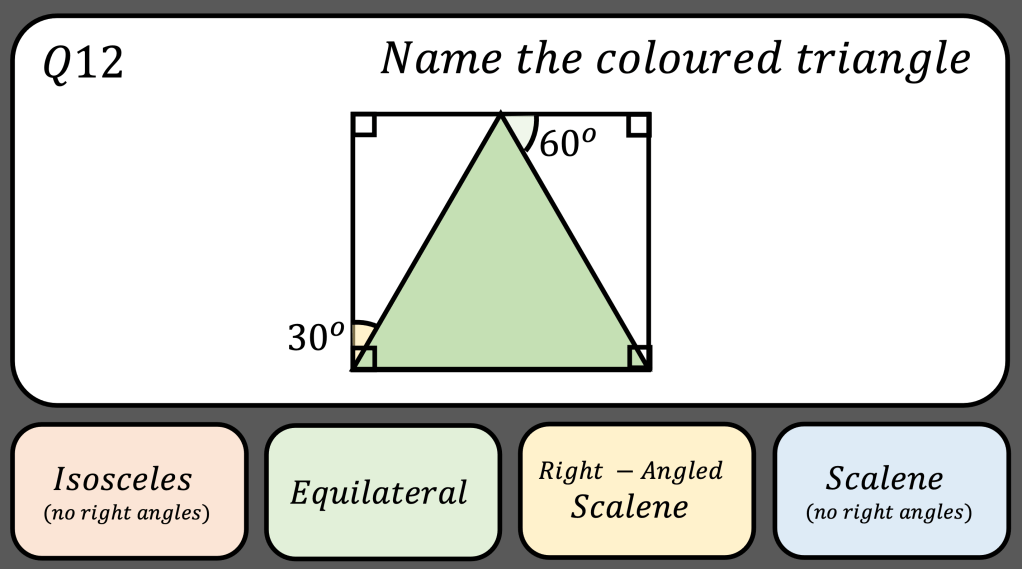
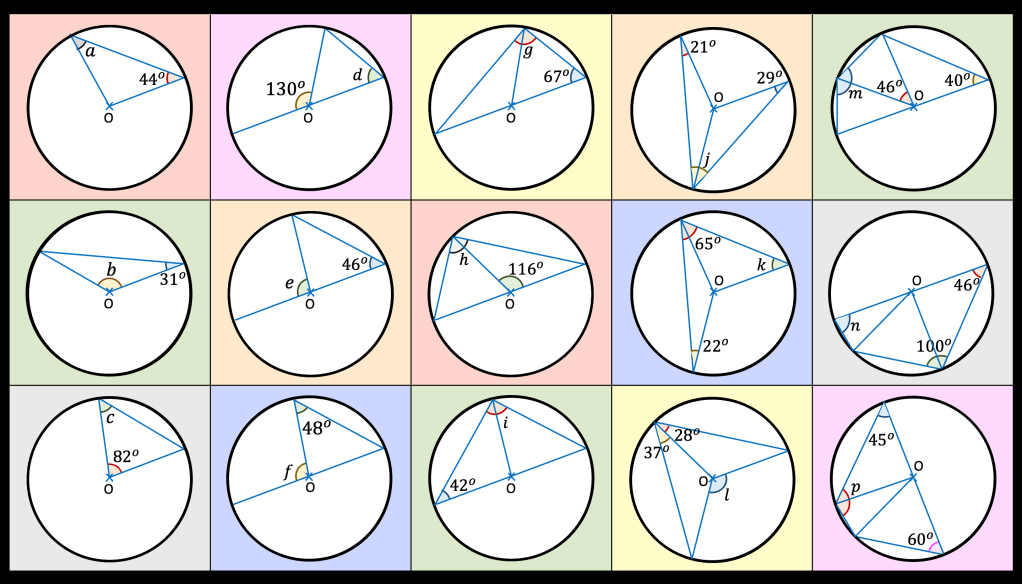
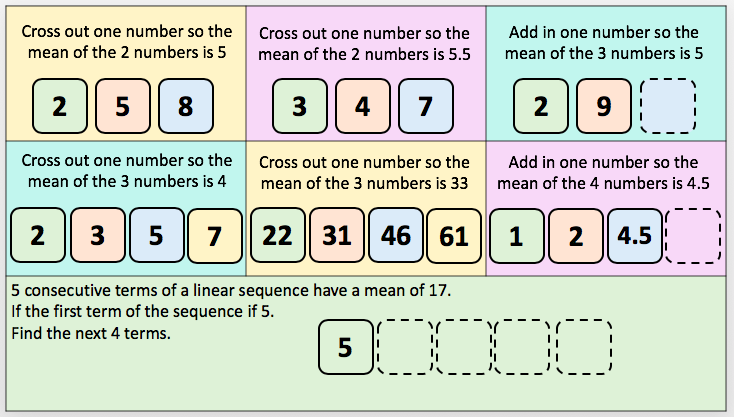
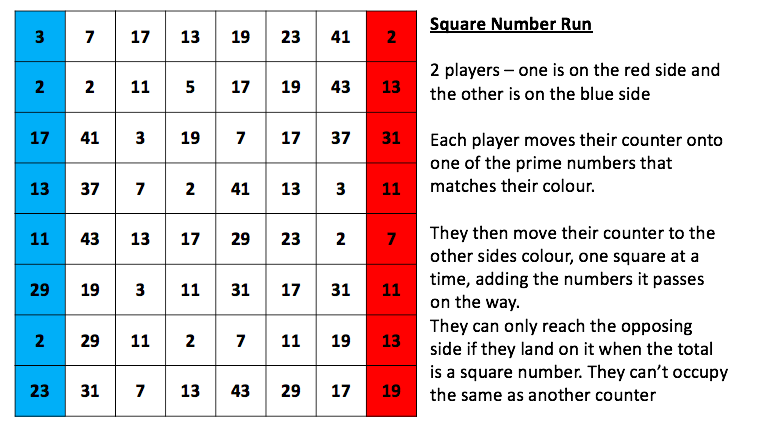
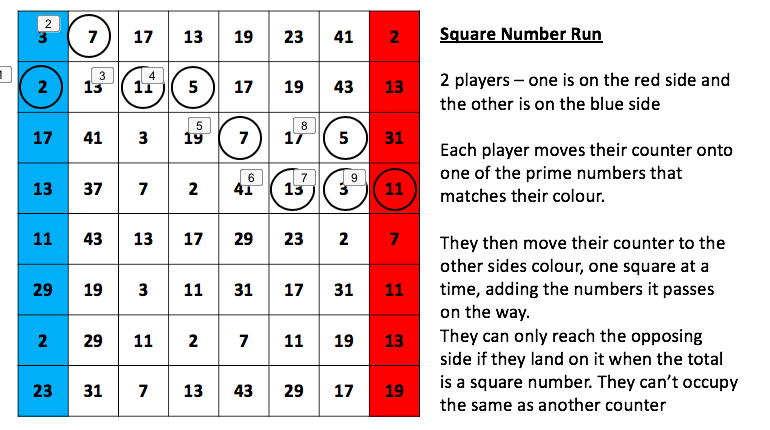
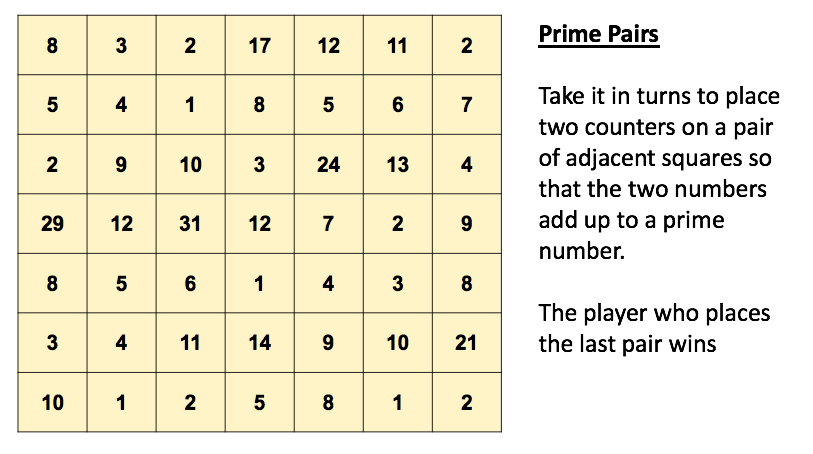
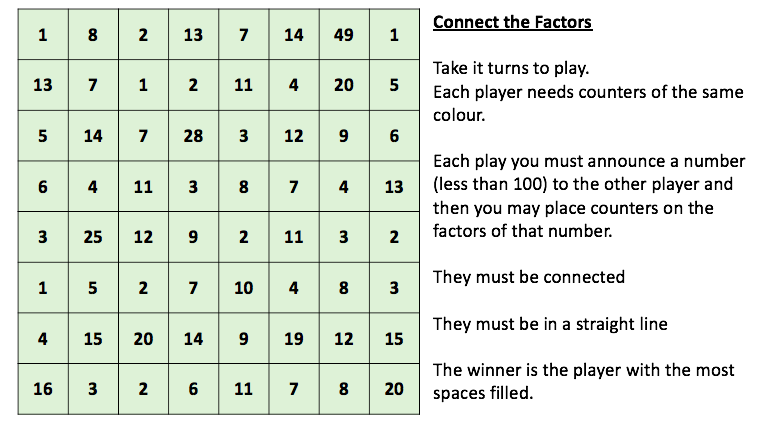
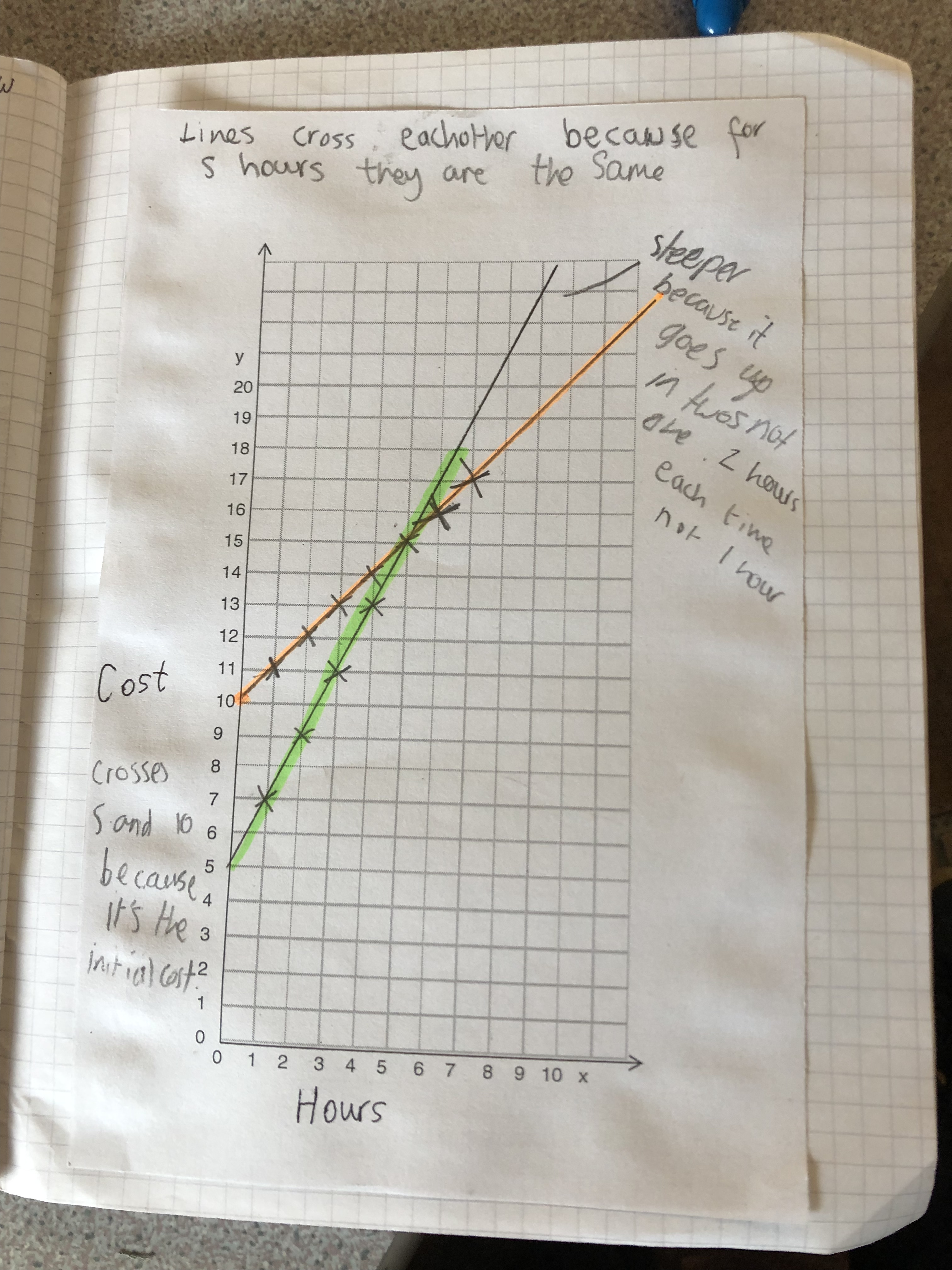
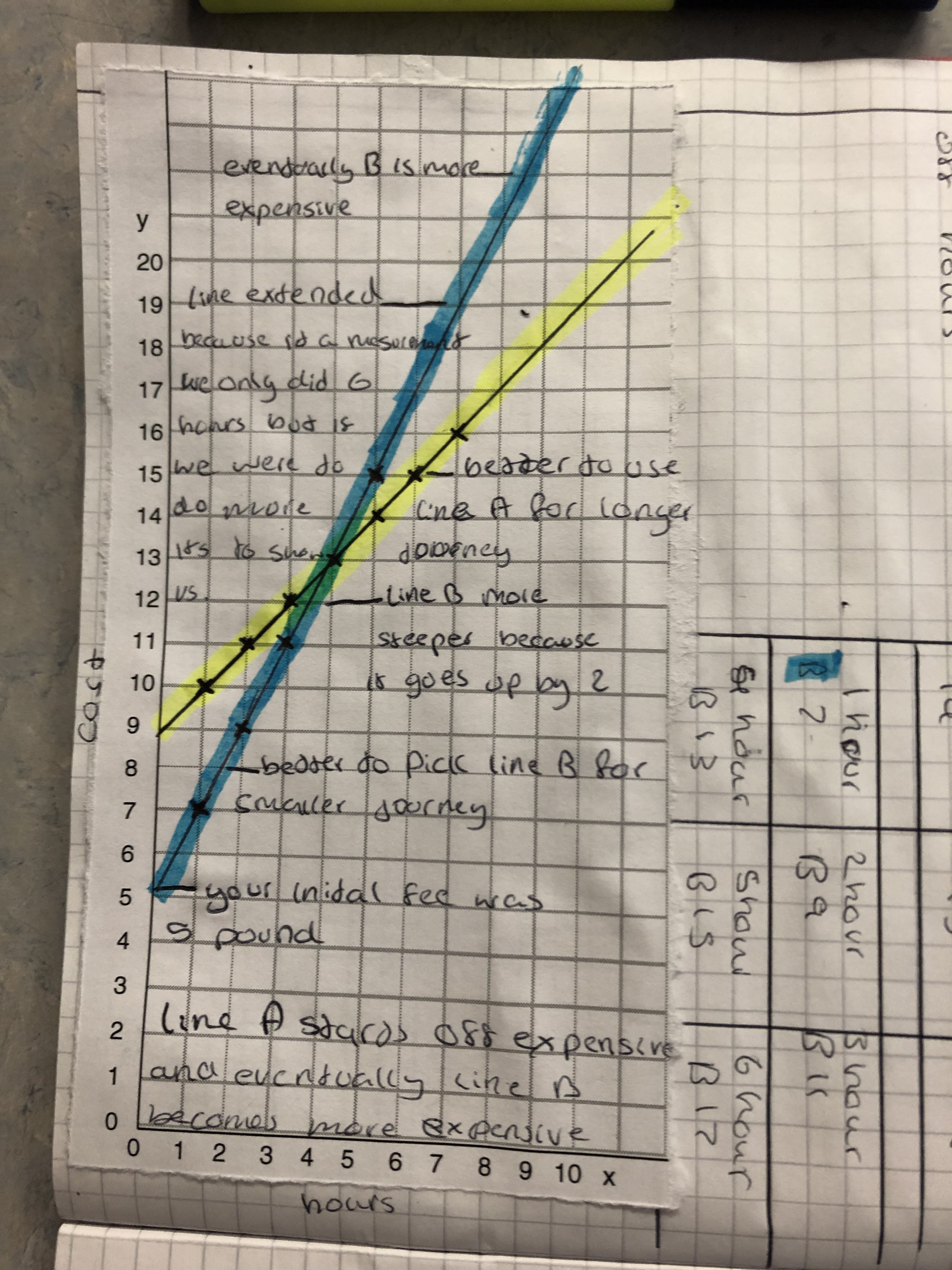
My daughter and I like to play a game called Penguin Pairs (memory I think people call it) but with matching penguins. It was a game that I played as a child and really enjoyed. If you don’t know it: each player takes it in turns to select two cards and turn them over to see if they match; if they do, they keep the pair but if they don’t they place them back faced down. The winner is the player with the most pairs.

After we have finished we have to figure out who has won. When my daughter was younger I’d announce, “you’ve won!” or “oh well, you lost but see if you can win next time”

Then a few months ago I didn’t say anything. My daughter said; “Have you won?” and I replied with “why don’t you tell me who has won?” She thought for a few minutes and announced she had, but without looking at the number of pairs. I said “are you sure?” So she reached across and started lining her pairs up with mine and looked at me and said “no, you won” I said “how do you know?” and she pointed to the extra 2 penguins and said “because I don’t have any to put here” (pointing at the gaps)

The next time we played it was in a smaller space and on a little table rather than the floor. We were faced with the same problem at the end: who had won?

Space was limited so during the game my daughter and I had made piles of our pairs rather than place them side by side. So when the game had ended we both piled up our cards and we looked at the two piles. She announced “we both won because my pile is the same as yours. They are both the same tall”

Last night we played the game again after a month of not playing it and we played it on a gymnastics mat. Without discussing it we had both placed our pairs in a line along the edge of the mat. I’m not sure who made the decision to do this but we ended up two lines side by side. She said that her line was the longest so she was the winner. I did question whether a longer line meant she has won so she counted the lines to double check. Her line was 11 penguins and mine was 5 so she had won.

I was team teaching with a trainee today and she asked a question similar to the bottom middle question. The students found the unknown angle to be 70° and she asked ‘how did you know you could halve 140° to get the unknown angle?’ Students gave the answer ‘you take 70° from 180° and then you always halve whats left’ The trainee questioned that ‘do you always halve? What was it you saw in this question that let you know you could do this?’

So It made me think about questions that could have answer of 70° sometimes, always or never.

https://babbey-my.sharepoint.com/:p:/g/personal/konstantineh_barkingabbeyschool_co_uk/EcKqQNtNGYBJge7Uq0QUT4UBN4bpe64hEvkHwcBXDKIdTg?e=kThjhy

After a post on Twitter by @mathsjem https://twitter.com/mathsjem/status/1381970532912885764

I started thinking about angles in triangles and how its used in other areas of geometry. I had already looked at angles around a point https://mathshko.com/2020/08/09/angles-in-a-full-turn/ and angles on a straight line https://mathshko.com/2020/10/26/angles-on-a-straight-line/ in this way. I had taken some time to link angles in straight lines and round a point with pie charts, clocks, bearings and angles in polygons but hadn’t looked at angles in a triangle in the same way. Jo shared some exercises from an SMP book and commented on its being “a nice idea” and that she currently (typically) covers a huge chunk of circle theorems content in one go, often in Year 11″ and “why not introduce one or two earlier? Particularly isosceles triangles in circles” So I looked at questions where you could use the angles in and isosceles triangle but also discuss other ideas from the solutions.

I’m not going to discuss circle theorems with year 8 when I use this but just let them use angle in a triangle/isosceles triangle to work out the angles – we can discuss what we notice after

Some questions that use Mean or i suppose they actually require students to realise that in order to find two numbers that have a mean of 5 the total of the two numbers must be 10. Students then select the two values that satisfy the totals.

Mean

The first game shown here is Square number Run. The premise is to make a path across the grid so the total is a square number. The first to reach the other side wins.

This can be adapted. Maybe it works better to keep the counters on each square you pass the other player cannot use that square after. I’d love to know how the game goes when you use it.

Here are all the games in ppt form

connect the factors

square number run

prime pairs

The next game is called Prime Pairs and each played places counters on adjacent squares so the numbers add up to a prime number. They keep taking it turns to do this until someone can’t go, the person who places the last pair is declared the winner.

The next game is loosely based on connect 4. Players announce a number (less than 100 – this could be changed but i figured if they multiply every value in a row then all the numbers in the row can be covered) and place counters on numbers that are adjacent and are factors of that number. The winner has the most squares covered.

UPDATE! I decided to trial two of the games ‘prime pairs’ and ‘connect the factors’ with year 7 today. They seemed to go down well and students seemed to be engaged. It did invite some interesting discussion about strategy (if there was a row of 4 numbers in Prime Pairs then students told me they placed the counters in the middle in order to stop the opposing player having a go)

After they played each game I gave the students 5 minutes to reflect on the games and how they might improve them. A selection of the most popular improvements are below. This will form a discussion for the next lesson

‘can you have diagonals in the prime pairs game?’ i was considering allowing diagonals and see if they notice anything. I might let them create their own grid to play with.

‘Should we only allow 3 or more shaded for the factors game?’

‘How can we have got a row of 3 instead of two in this situation?’

‘What number(s) have 12, 9, 2 as a factor?’

‘Can you find a number who’s factors add up to the number?’

I wanted to make a question to practice Venn Diagrams with year 11.

Using colour will help the students describe the regions in class. I thought it might help getting instant feedback (using whiteboards) on which region they thought fit.

The object of this puzzle is to fit rectangles on the grid that are unique, have different areas and all of the areas are multiples of 3.

I wanted a task where students consider multiples and factors. They need to know which length have a product that is a multiple of 3 and also consider that all the areas have to fit on a 9 by 12 grid so the areas all need to add to 108

I saw a task where students had to play a game against a partner. They rolled two dice and multiplied the numbers together, they could then draw a rectangle on the grid with a perimeter equal to the product of these two numbers.

I decided to create a task loosely based on this idea but I decided I wanted to look at areas instead. I then realised my task wasn’t really about area but about factors. Students need to also consider which numbers have only one or two solutions. If students look at the first two areas in the list they should note that 14 has factors; 1, 2, 7, 14 but a 1 by 14 rectangle isn’t possible in this grid so it needs to 2 by 7. Likewise 3 by 9 is the only possibility here. Once they have drawn in 3 by 9 on the grid it leaves a thin rectangle with a width of 1 so 1 by 6 is the only rectangle that fits here (or a 1 by 1)

rectangles

64 is a FACTOR of my number

I have had the pleasure of using the ICCAMS lessons and in particular Boat Hire

It looks at comparing two different boat hire companies and every time i have used it with a class I have learnt something new. Students never fail to surprise me with their ideas.

I decided with my low attaining year 10 class that i would pose the following question (I left my ICCAMS hand book at home!)

Abbey boats charges an initial fee of £10 and £1 per hour for using their boats

Barking Barges charges an initial fee of £5 and £2 per hour for using their boats

Miss  Konstantine wants to hire a boat, which should she use?

I gave students time to ask questions and make sense of the question i had posed.

Here are there initial thoughts:

I found the last students work quite interesting. He had used a rather nice way of recording the information for 1-5 hours. He was also able to determine which boat company to use for 1-4 hours and that both companies were the same price for 5 hours.

We used his work to move forward with the question and we discussed some of the other comments students raised at this point in the lesson.

We moved on to plotting the two boat hire companies and students naturally started to question. I asked for the class to share any questions they had about the graphs and if anyone wanted to, they could comment on what they noticed or thought.

Below are some of the comments and questions students had at this stage

I made the following problem to be used with my year 9. The boxed value was an error and they had to correct it. It also gave students a chance to discuss misconceptions.

I tried to include one where students used the Scale factor for length as 2 and the SF for area as 2

One where students correctly worked out SF for volume but then the length was halved not doubled,

Another question I included had the SF for area being used on a volume

then a question with SF for volume being used instead of area.

I then started to consider some more challenging questions that combined several ideas involving similar shapes, Scales factors and proportion.

Similar Shapes

What fraction is shaded?

Fraction Shaded 1

I was looking to review the mocks with year 11 and decided instead of working through each paper, I’d work through by related topics.

I noticed Ss in my class had trouble with finding of amounts when you ended up with parts. They also didn’t notice things in diagrams like 3.5 shades out of 7 is a half or 3.5 out of 14 is a quarter. They didn’t seem comfortable with decimals in fractions

I hope students are able to find the fractions shaded in the images below