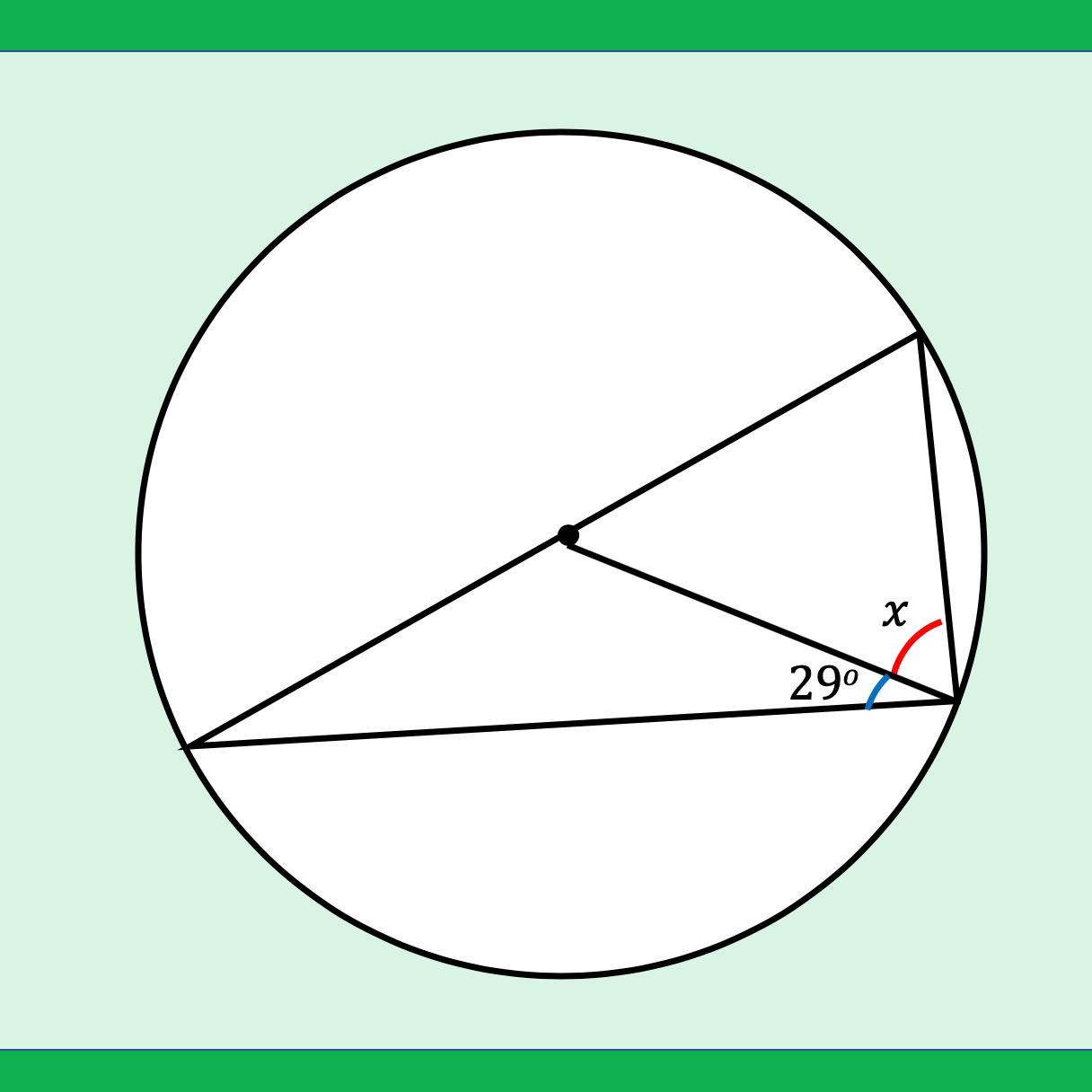
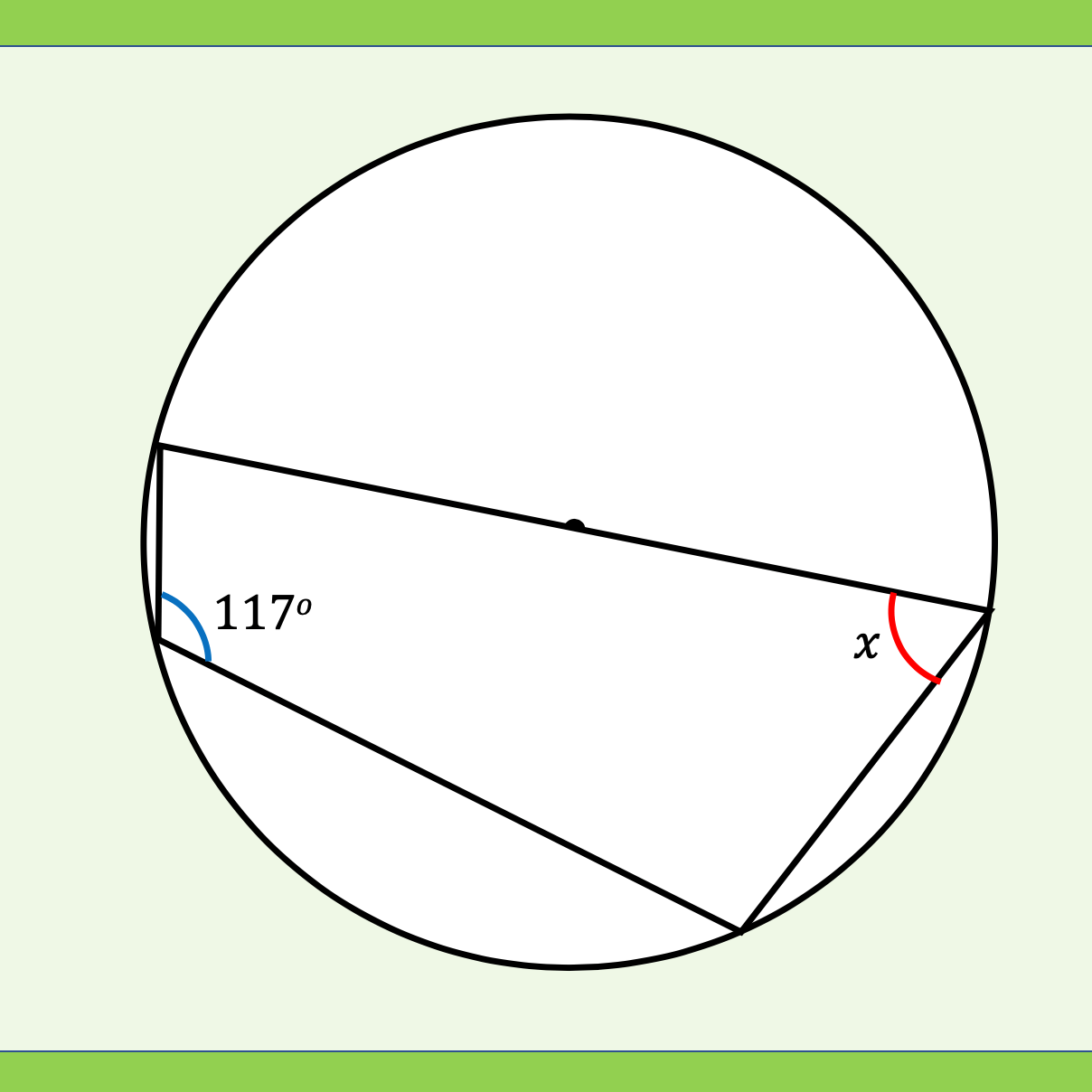
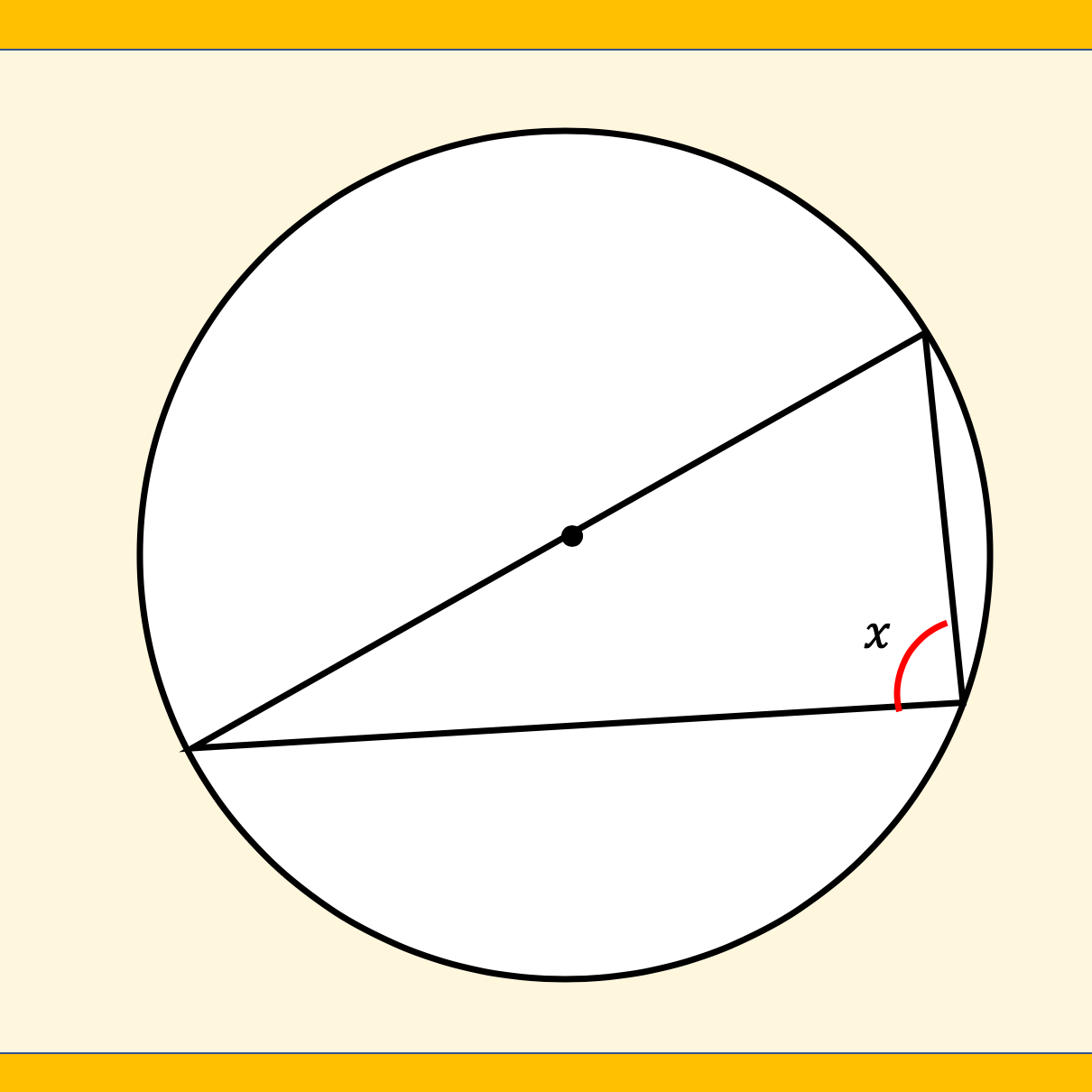
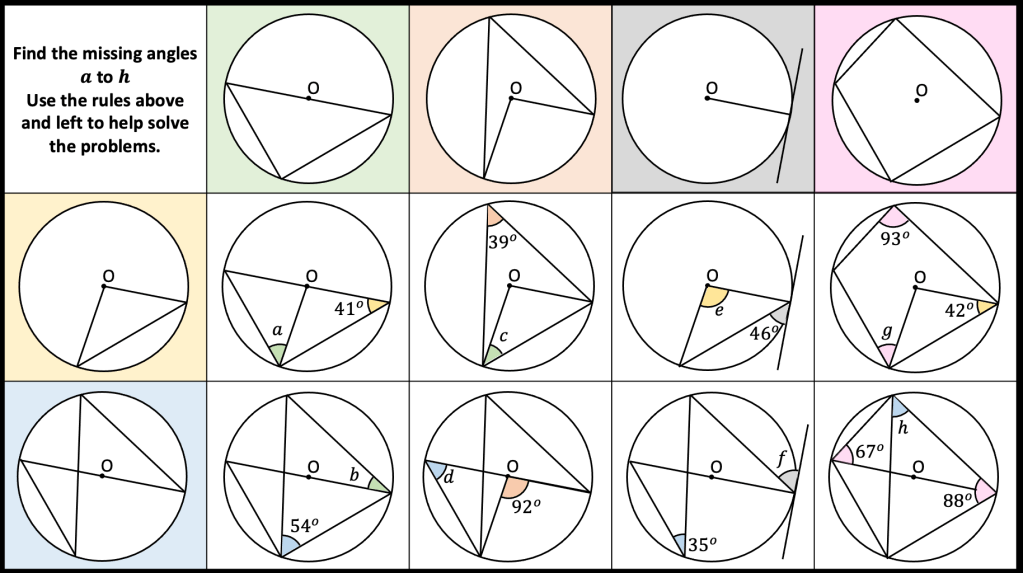
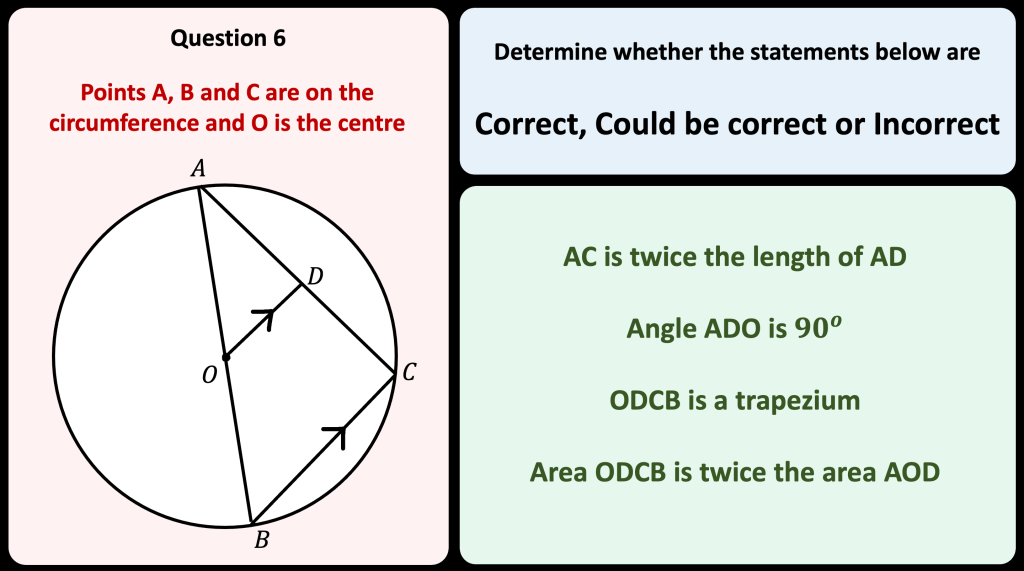
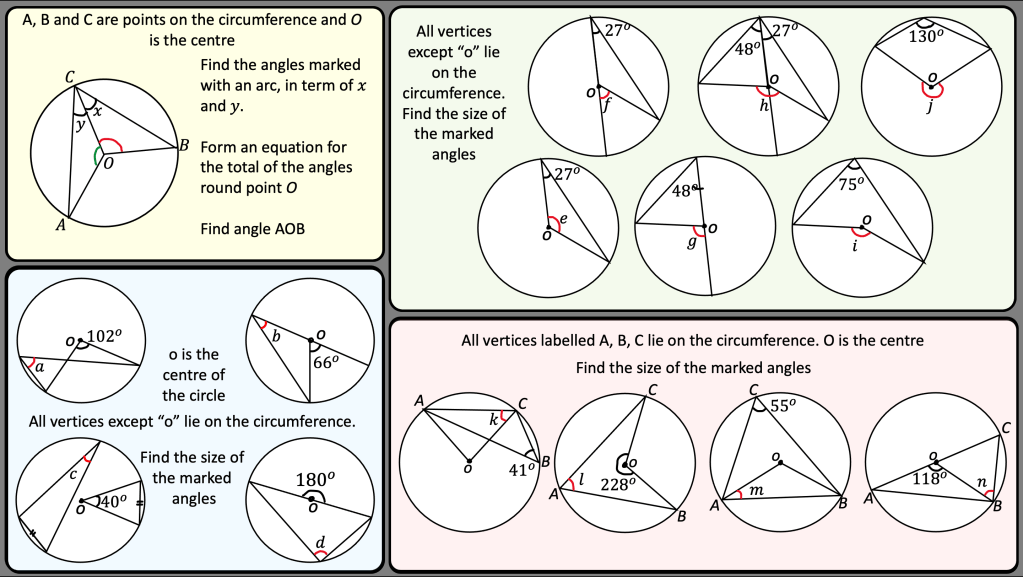
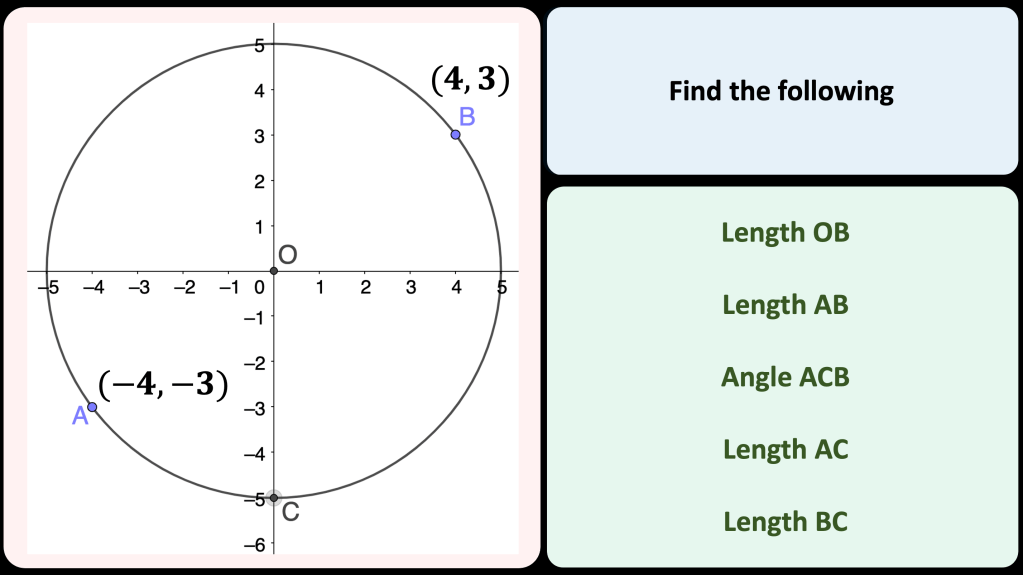
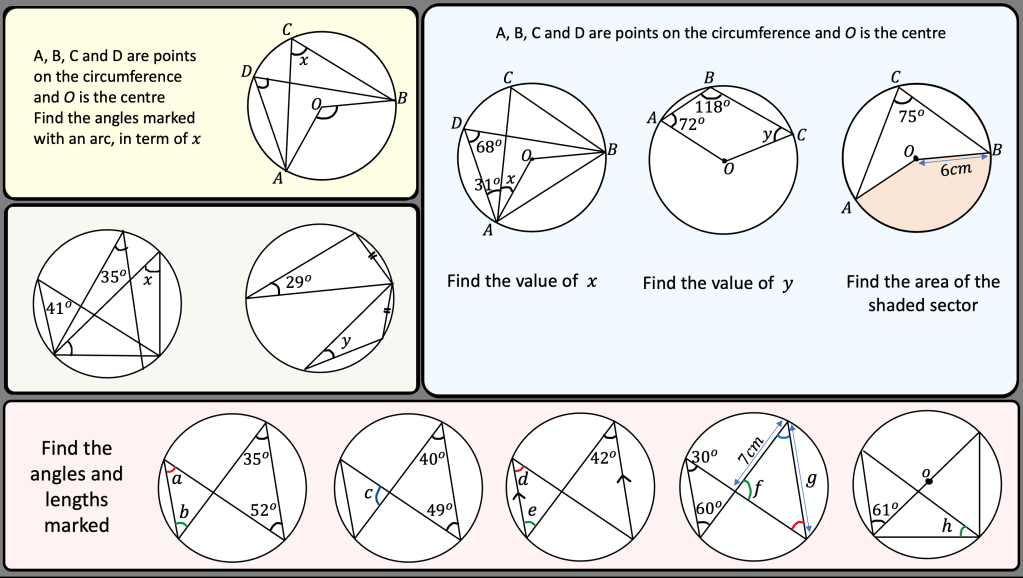
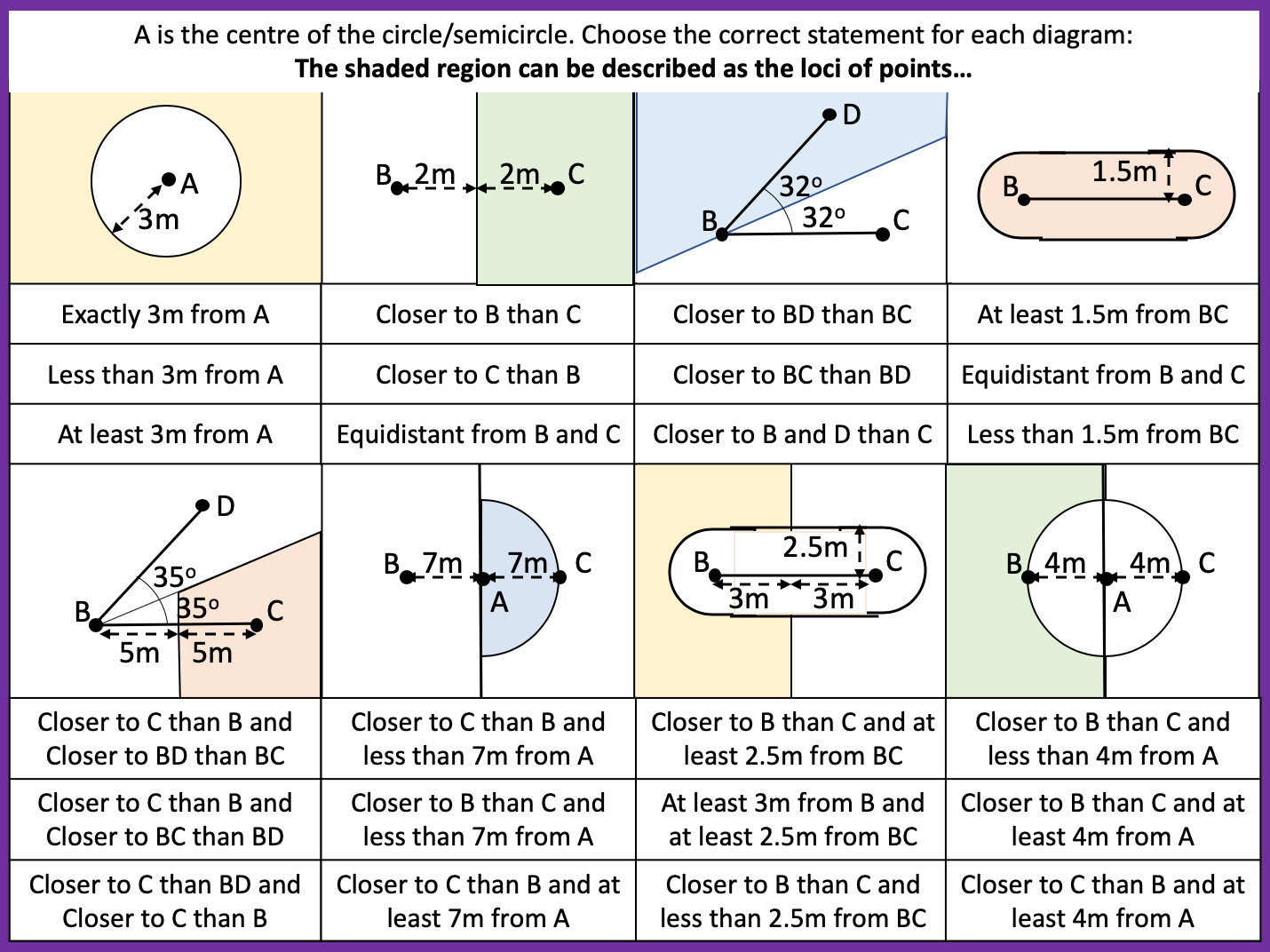
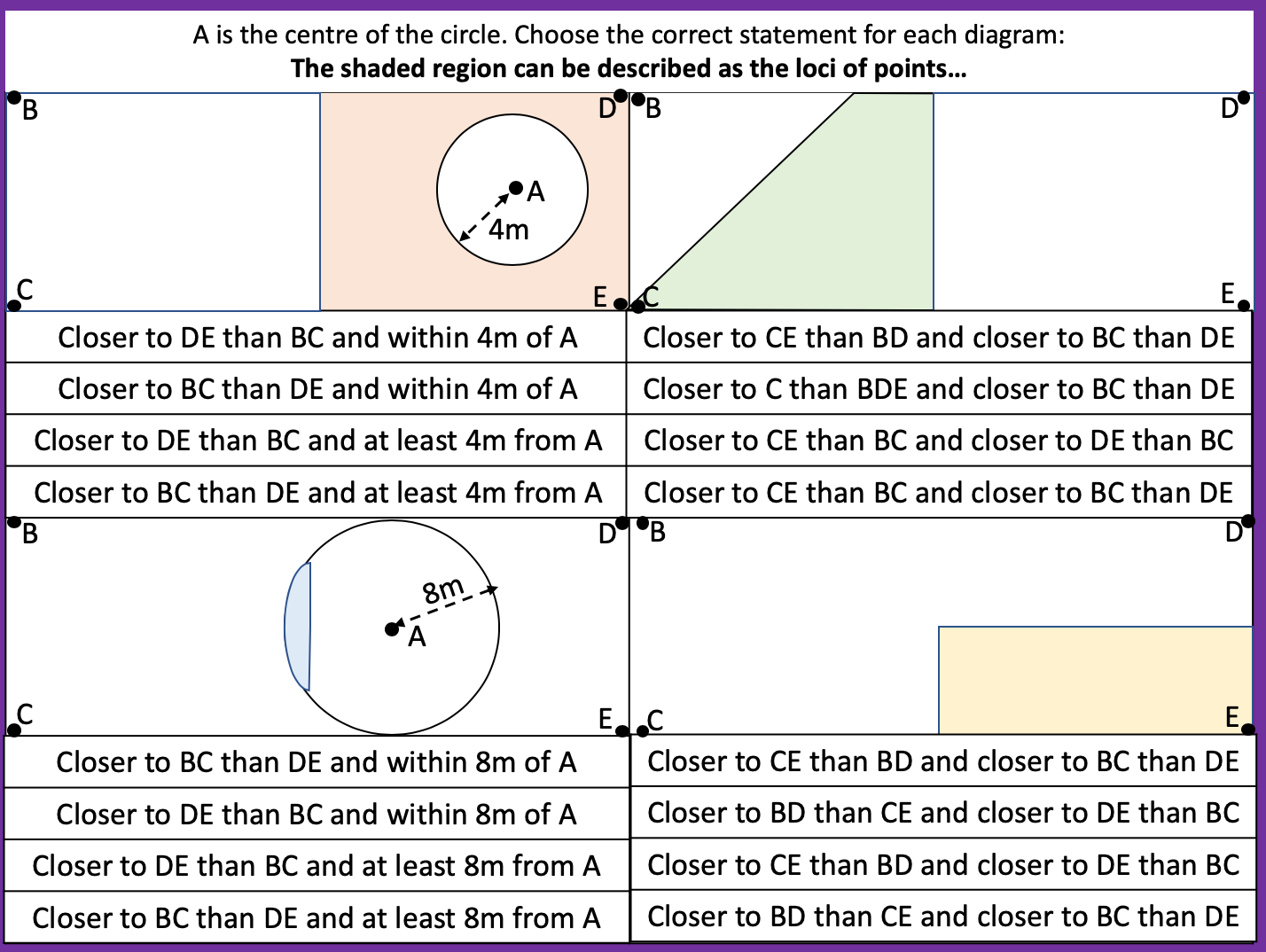
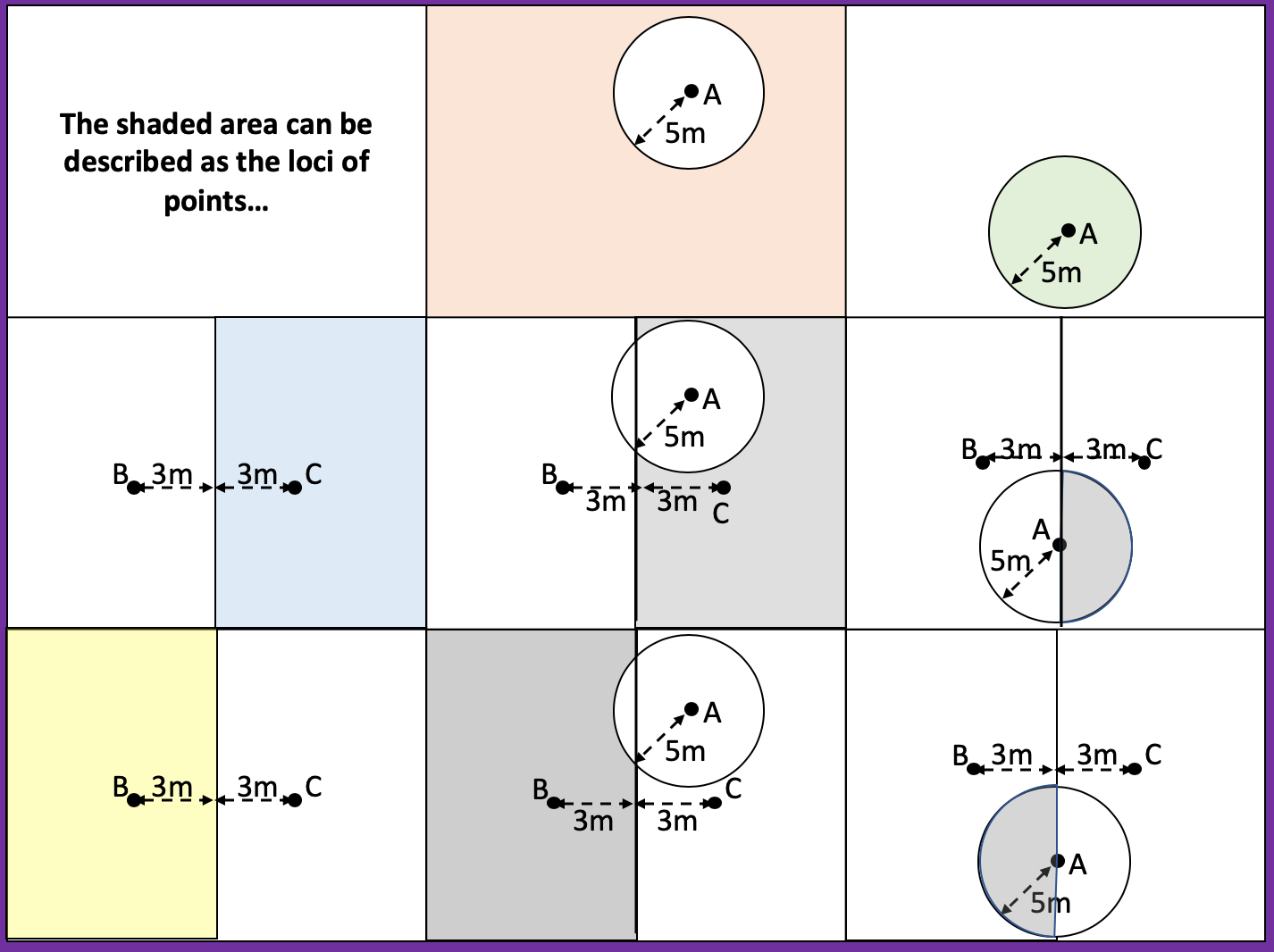
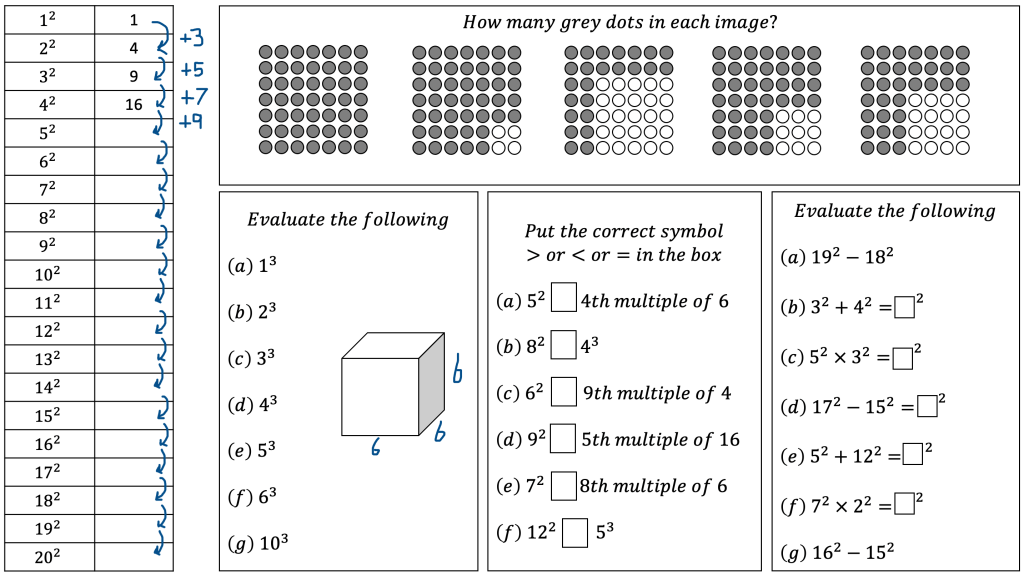
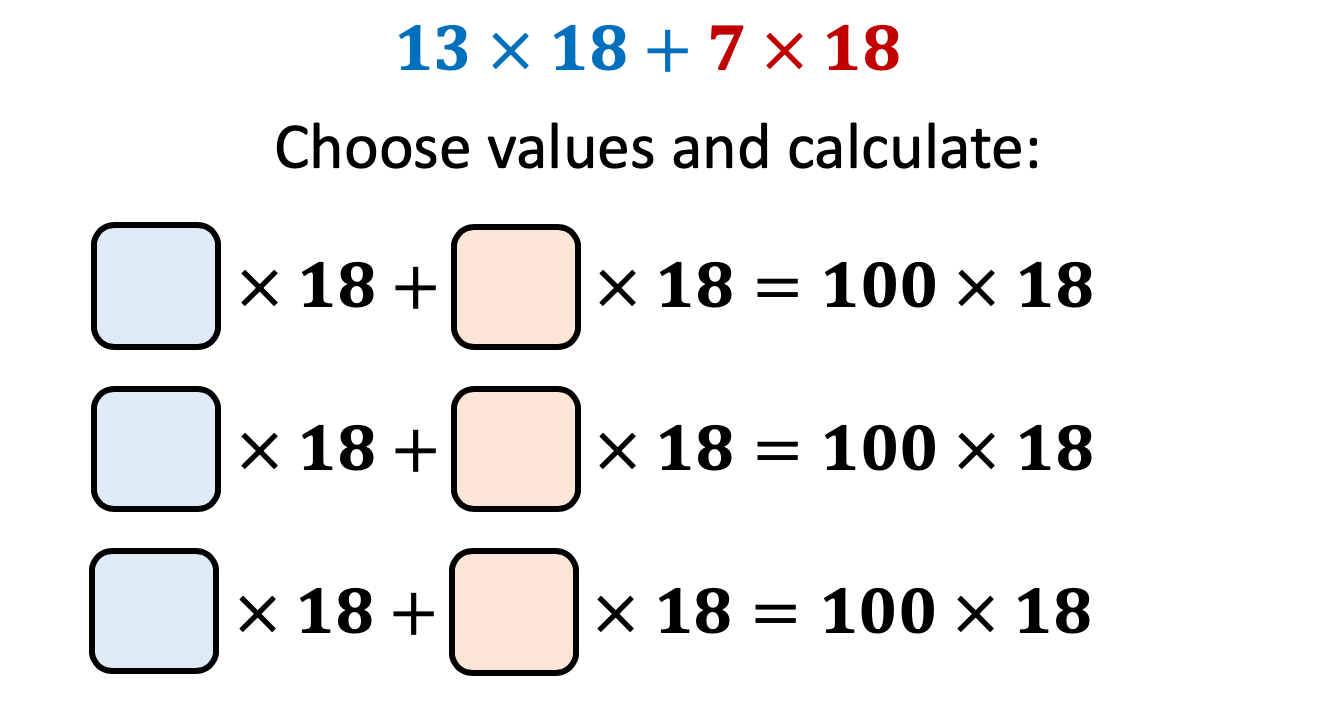I have been looking over this old image I made back in 2016. I wanted to look at different ways of viewing square numbers. The image at the top right is one of my favourite and I first saw it on the nrich website: https://nrich.maths.org/2275
It led me to think about the difference of two consecutive squares and the questions below.
I have been playing around with some ideas and questions on Area and Perimeter. I was looking at the changes to the perimeter when I doubled the length of one side and then looked at how it affected the area when a rectangle was enlarged. There is quite a difference in the difficulty of each question. Whilst I was looking at some of these ideas in Geogebra I thought about the idea of moving one vertex of a triangle, whilst maintaining the same area and what the possibilities were. I thought it might make an interesting question when looking at the area of a triangle. I usually start looking at the area of a triangle by using a prompt like the one below. I find it fascinating that moving one vertex of a triangle along the line parallel to the line joining the other two vertices always results in the same area. 
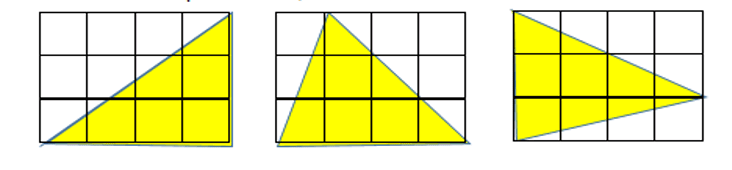
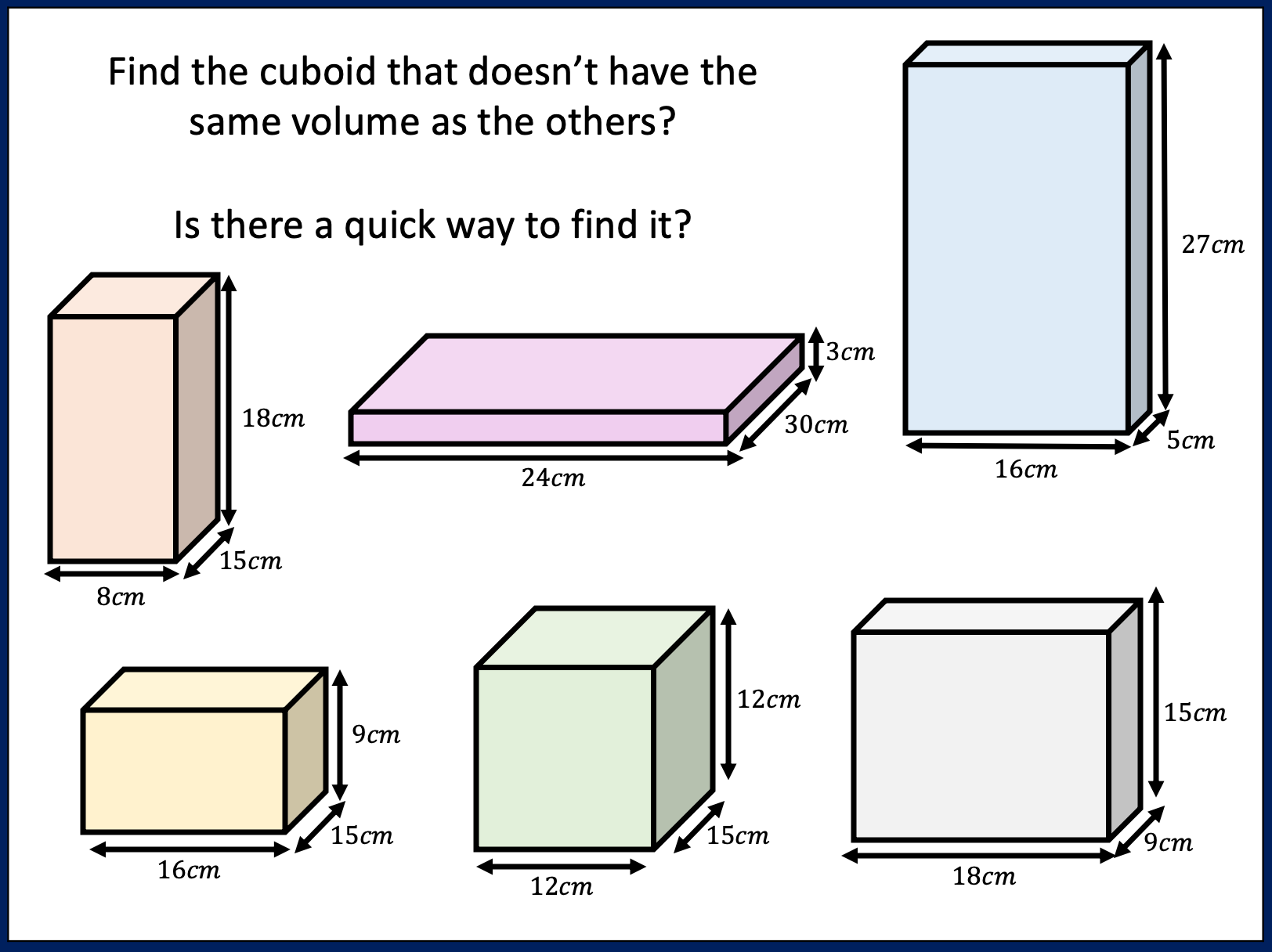
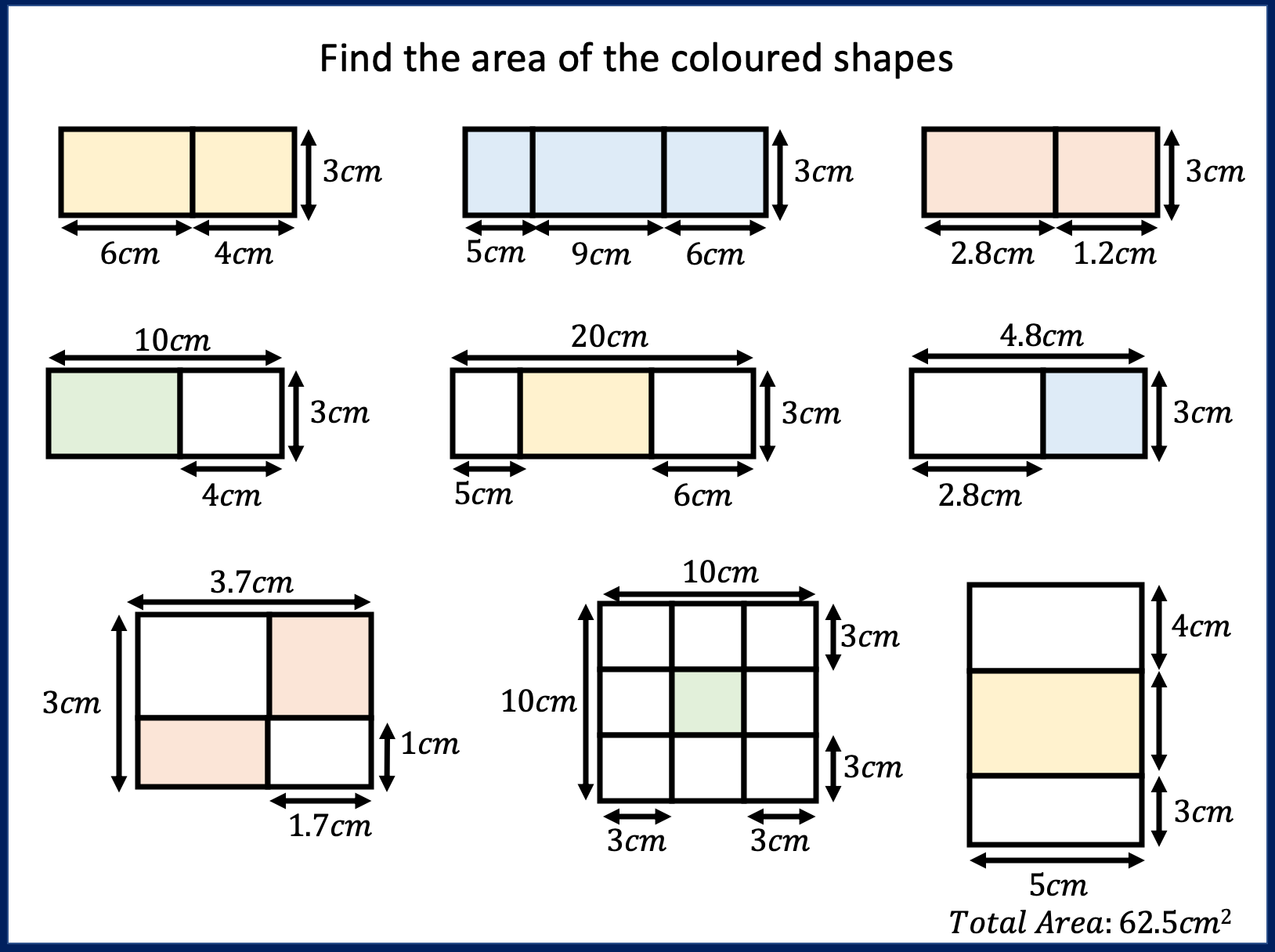
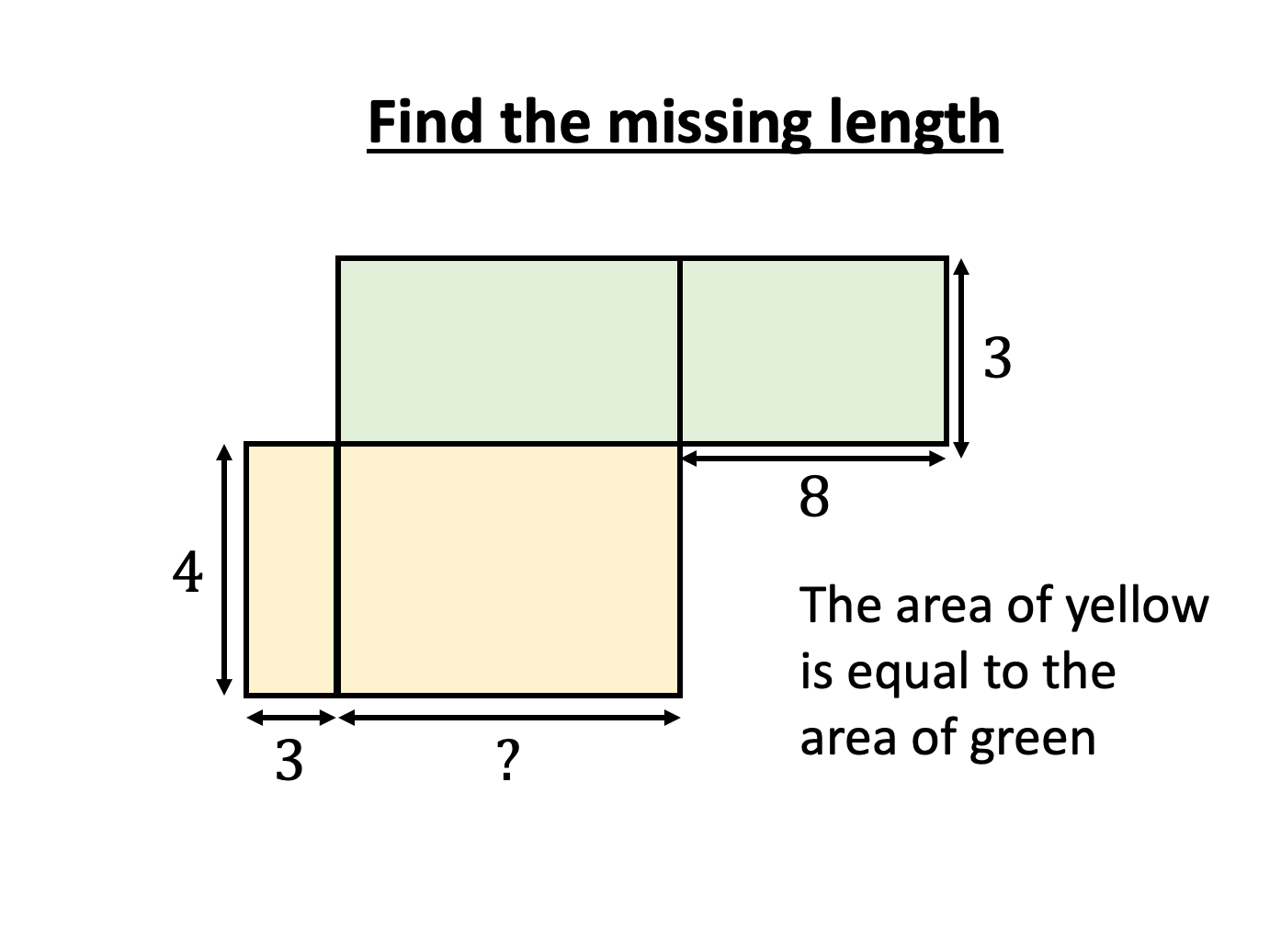
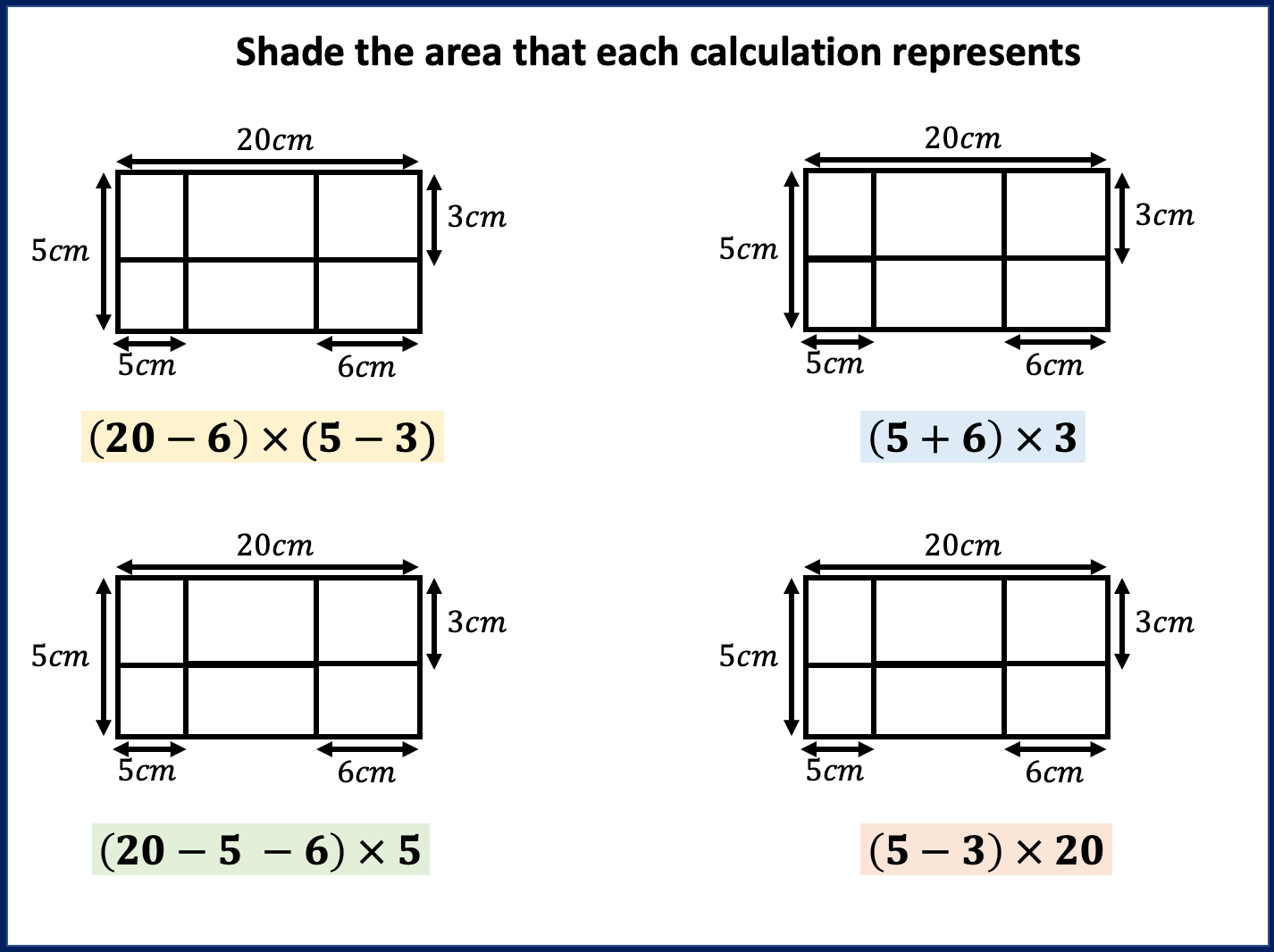
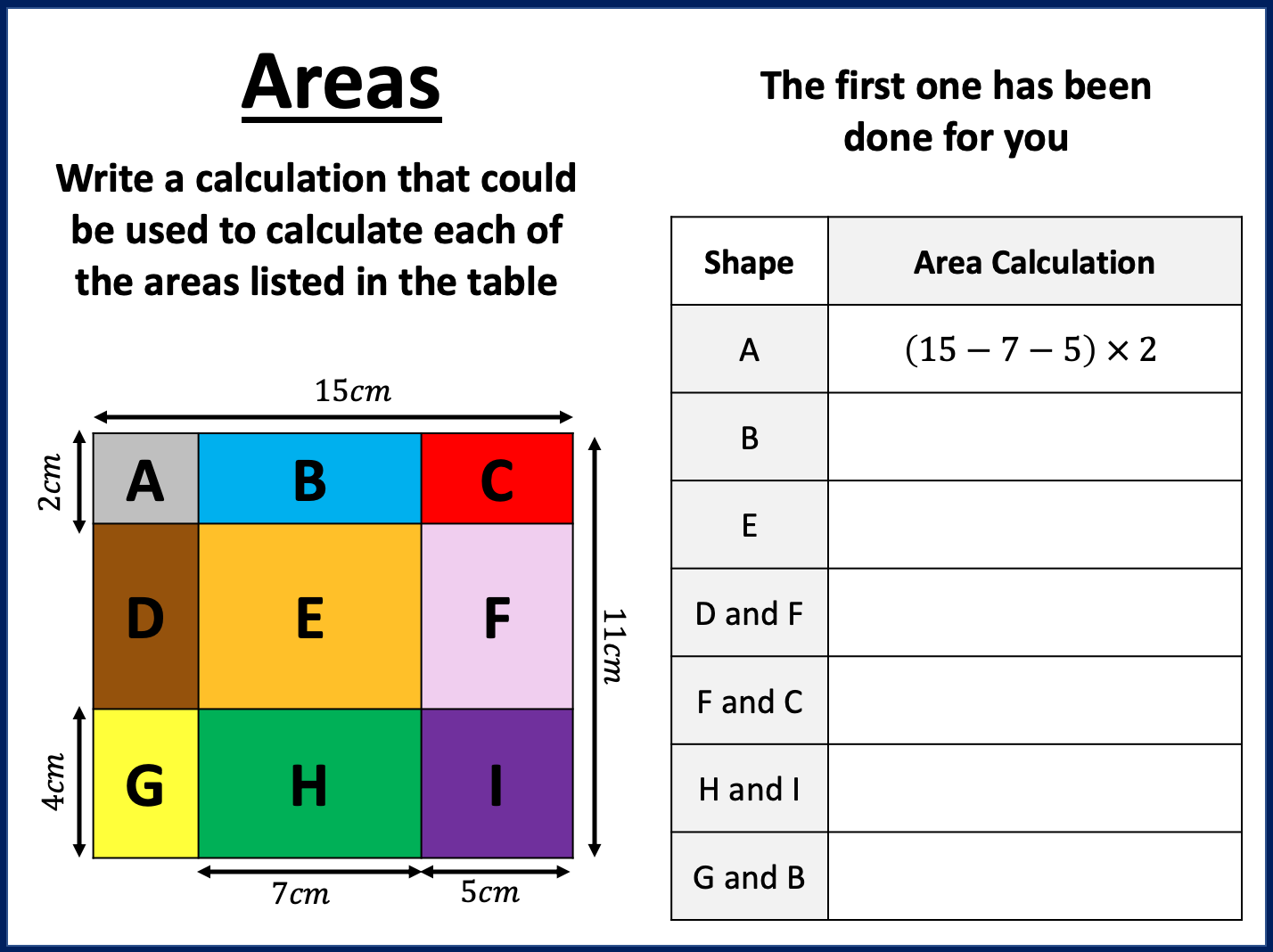
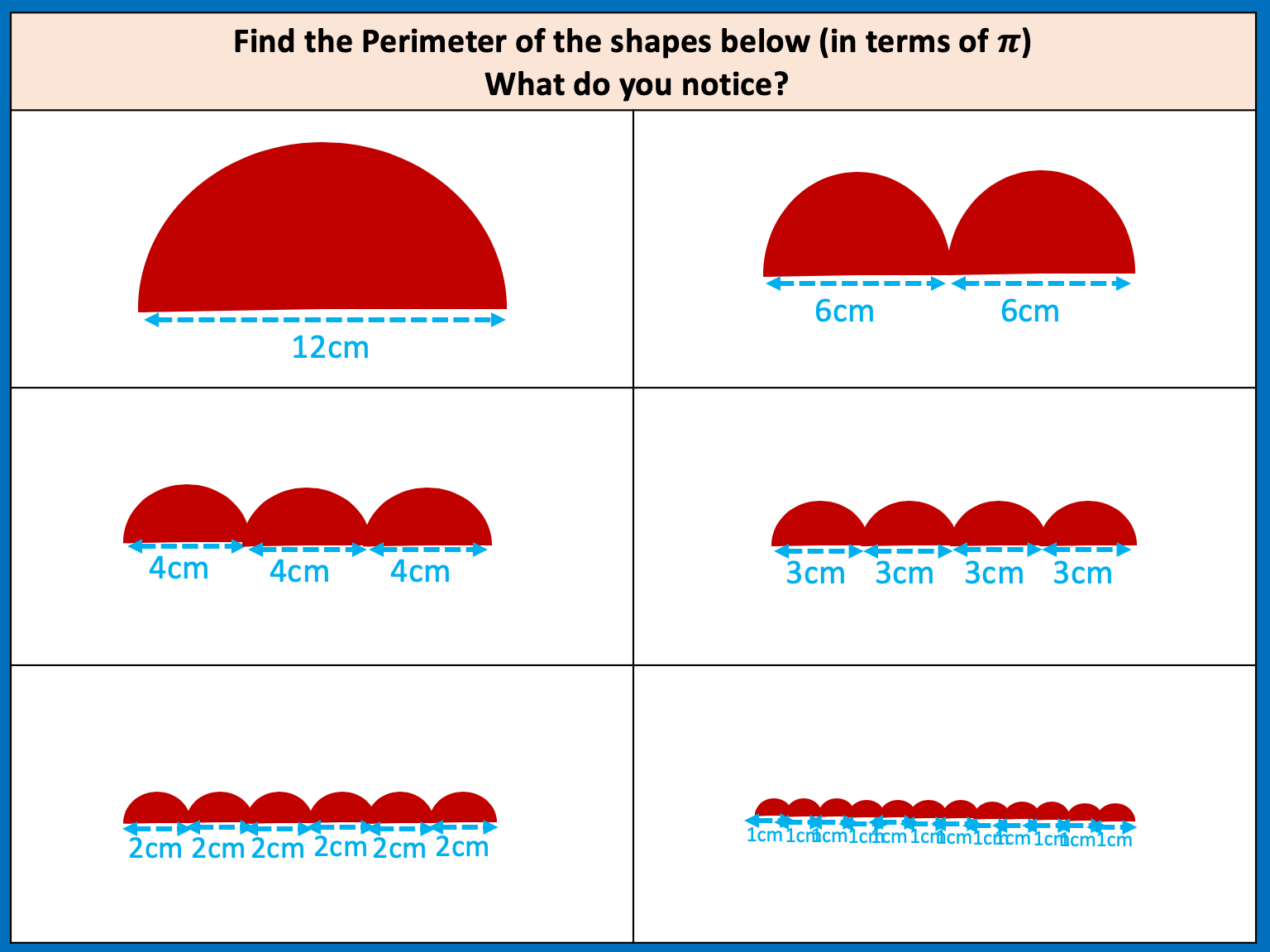
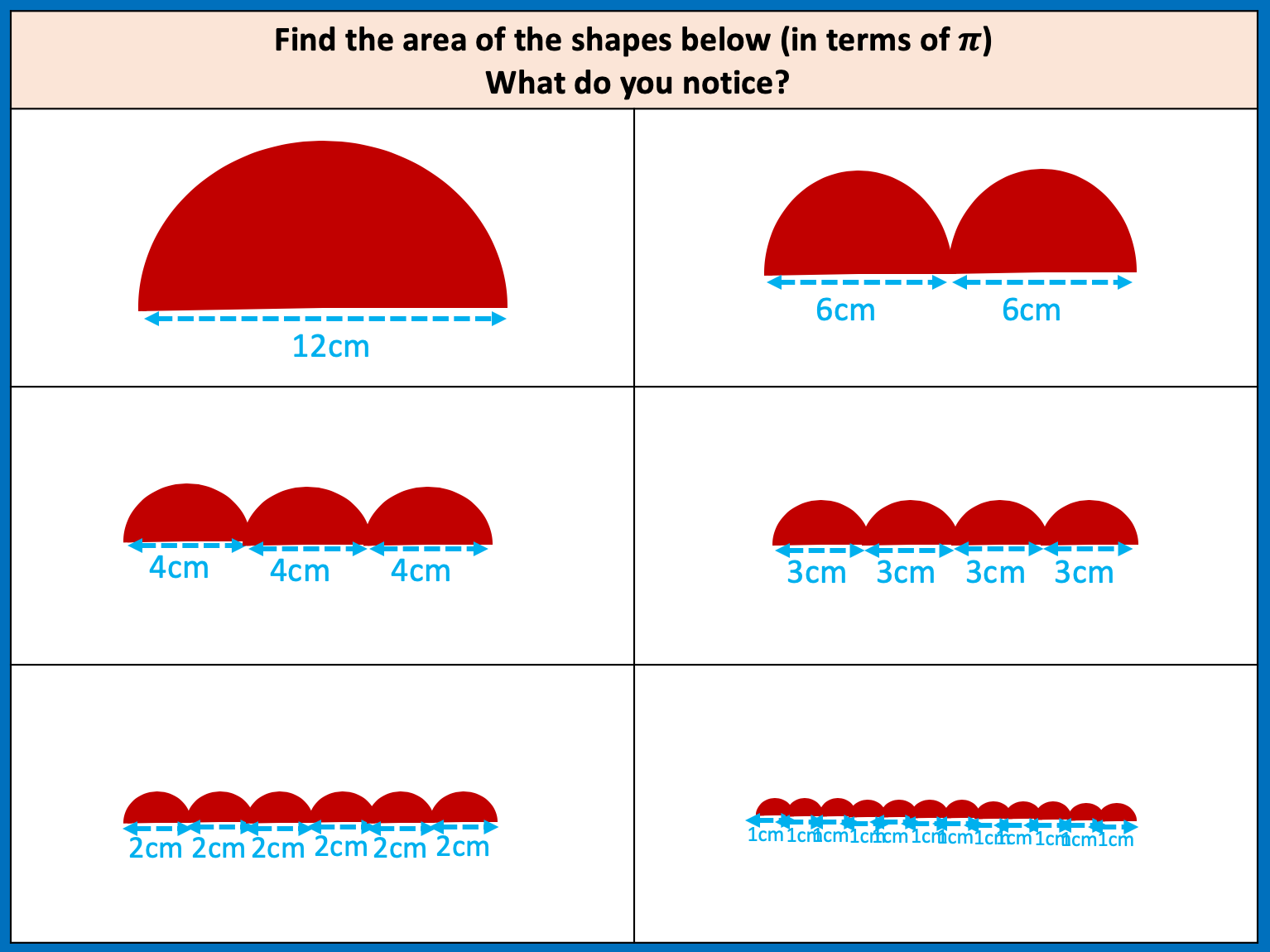
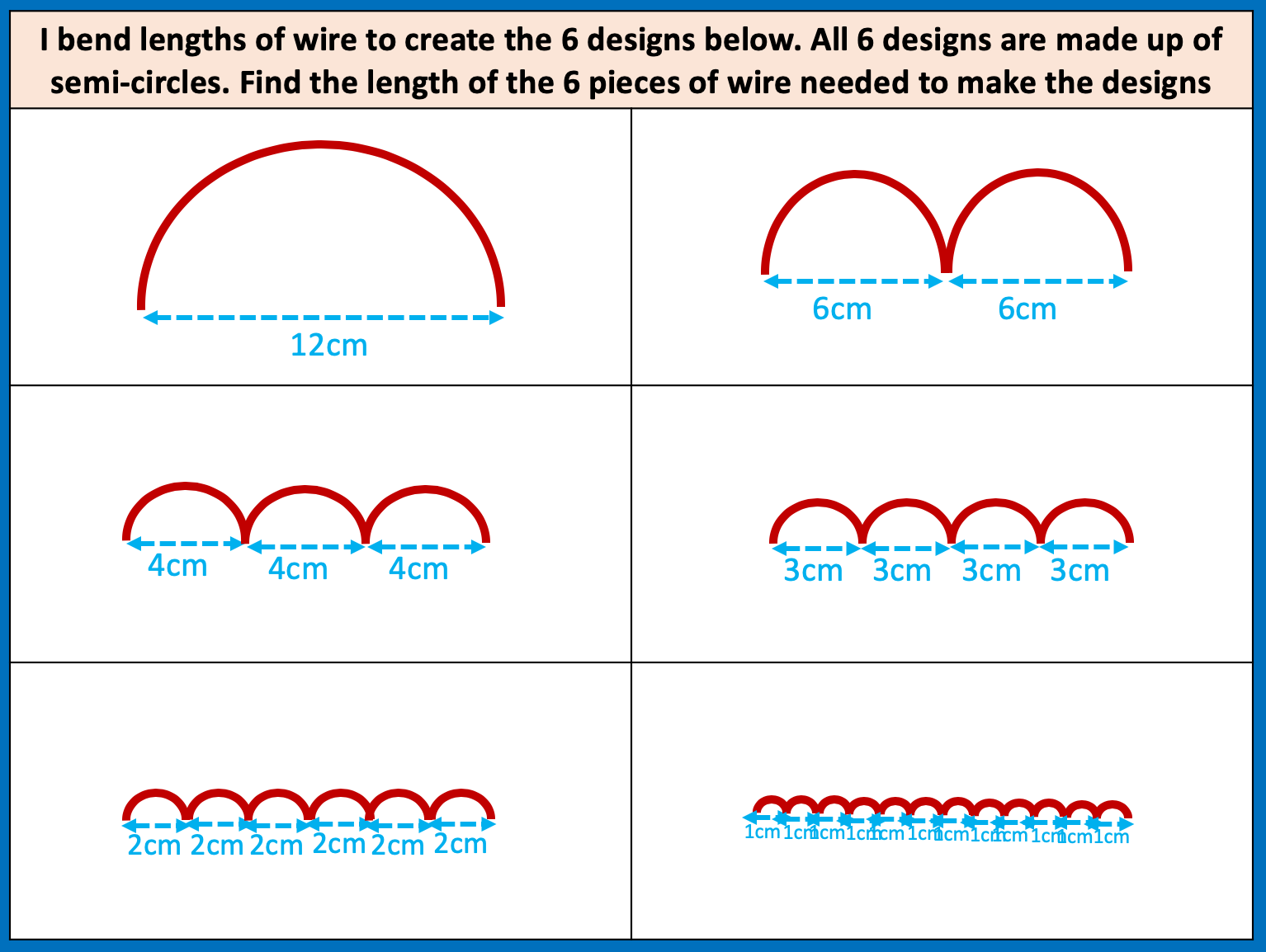
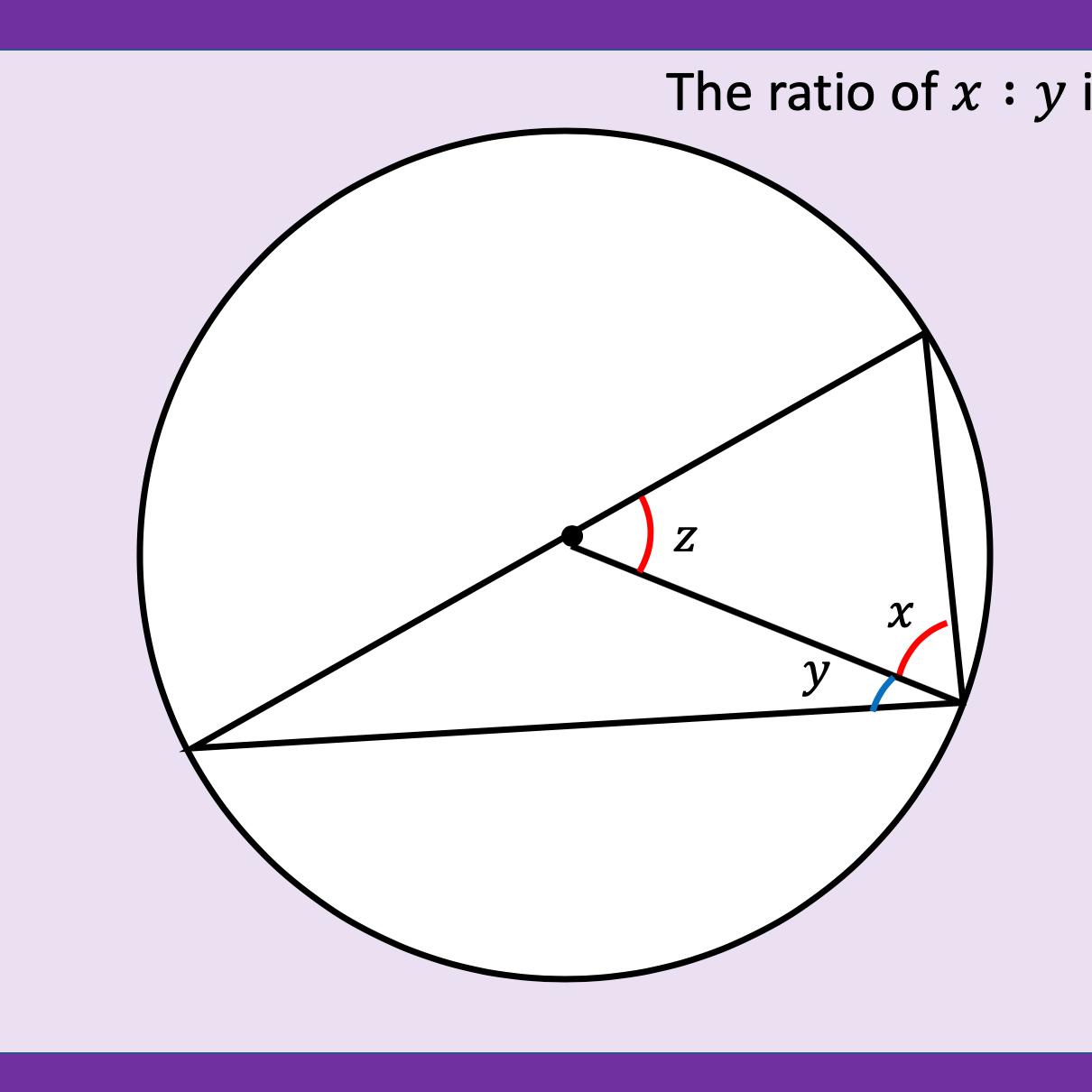
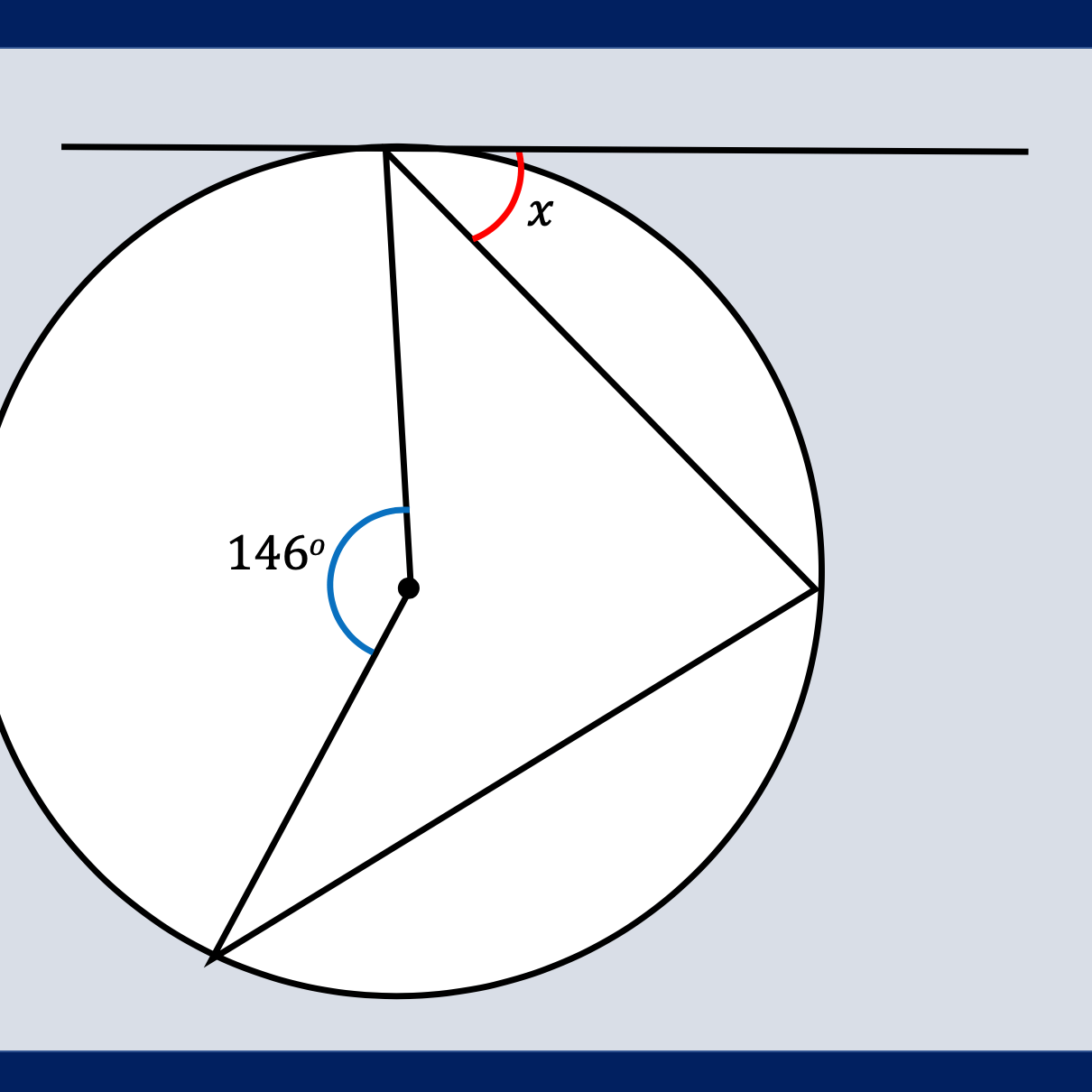
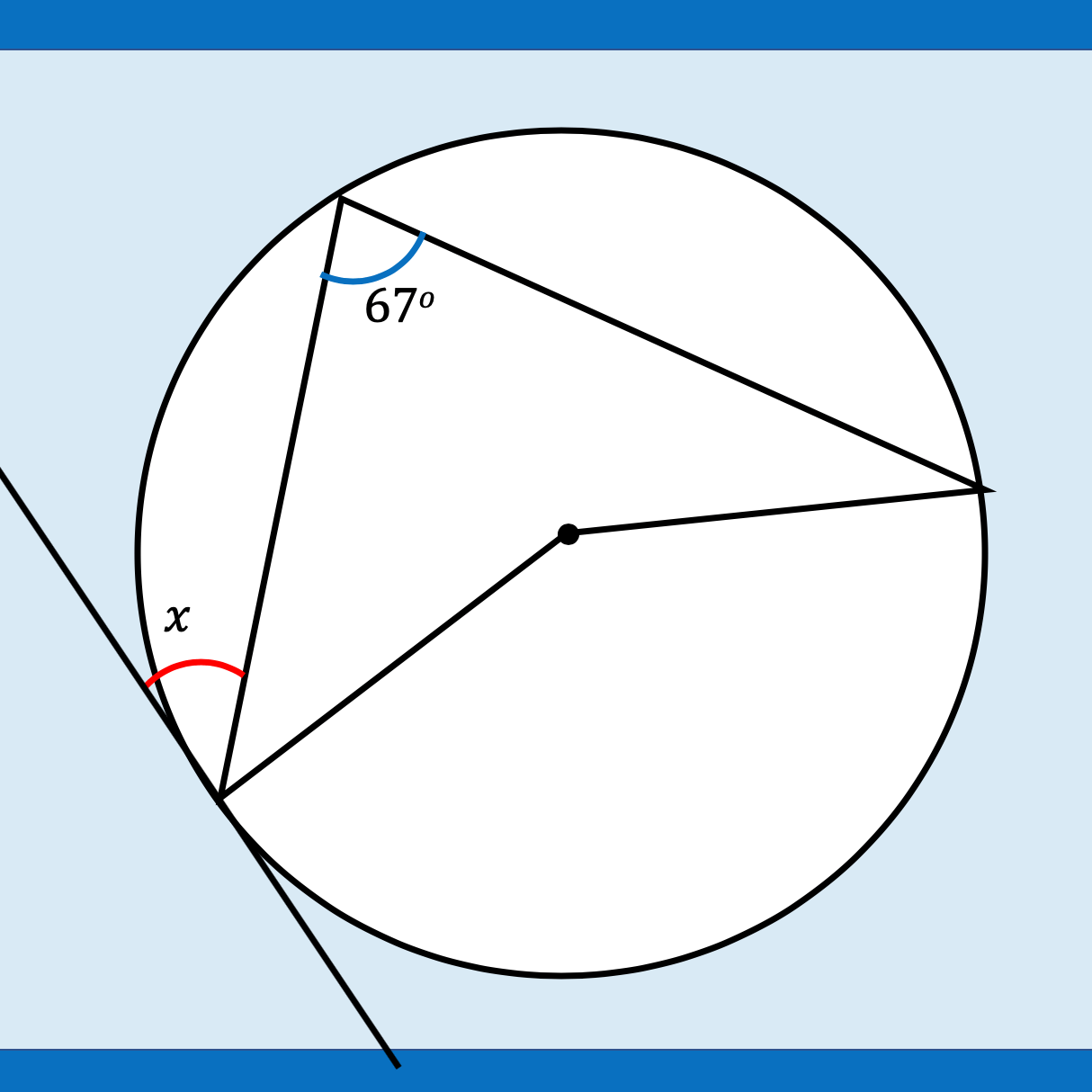
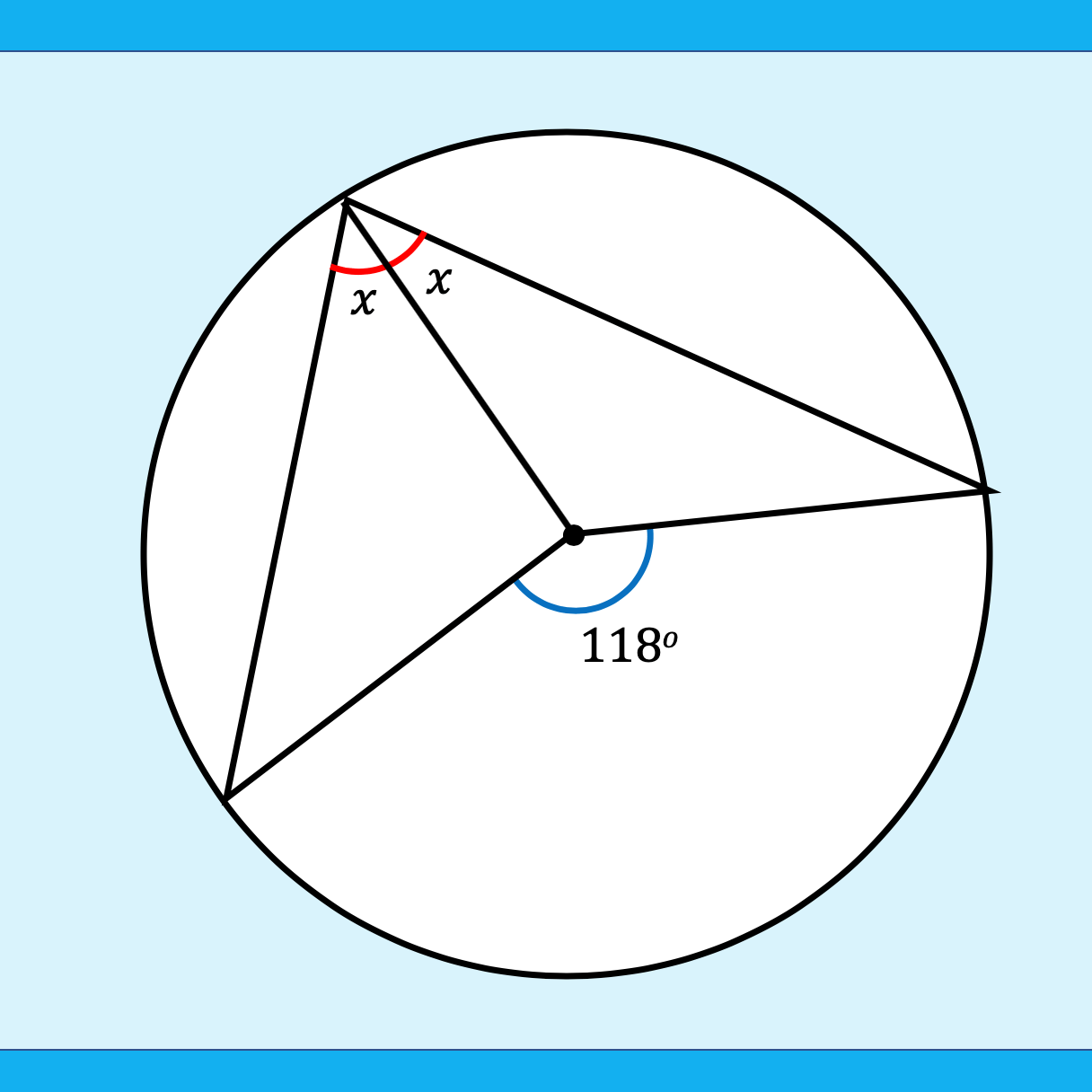
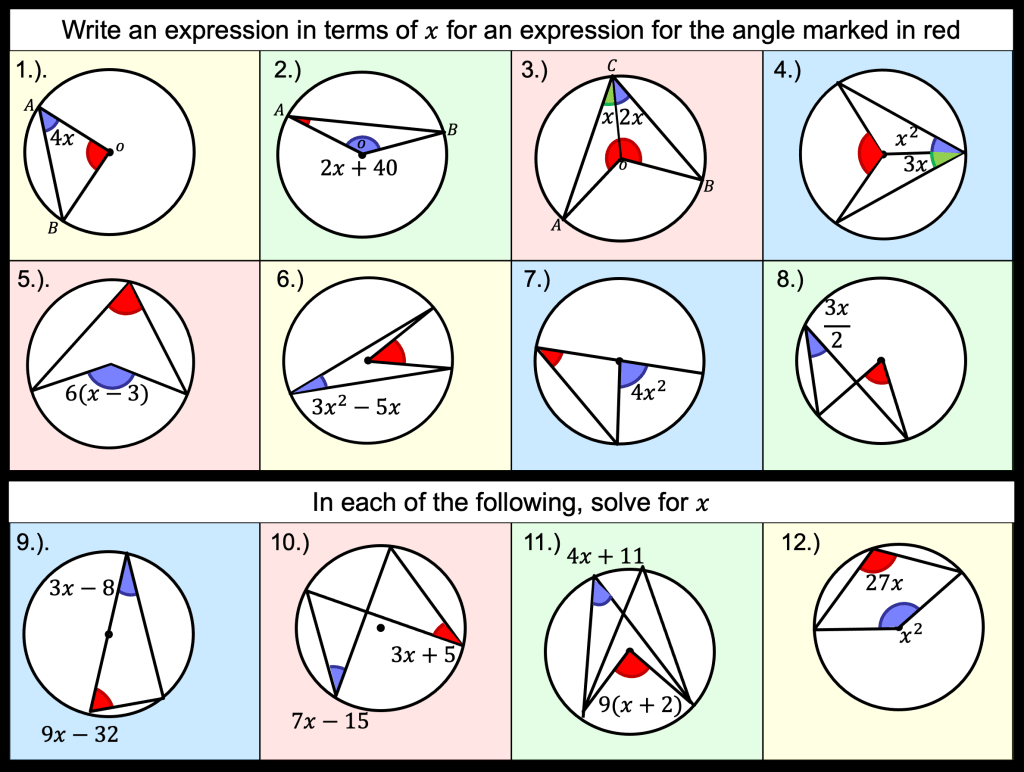
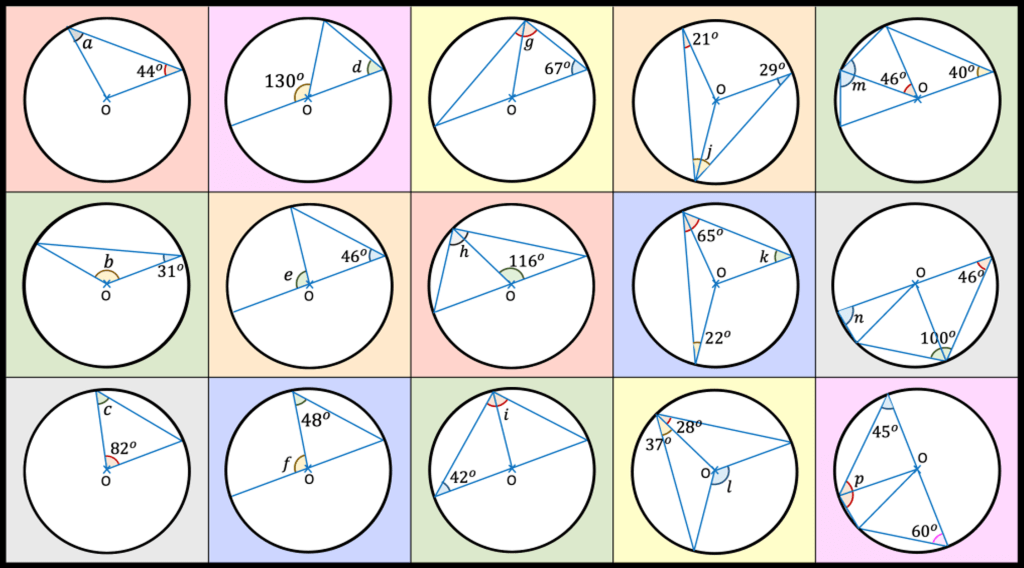
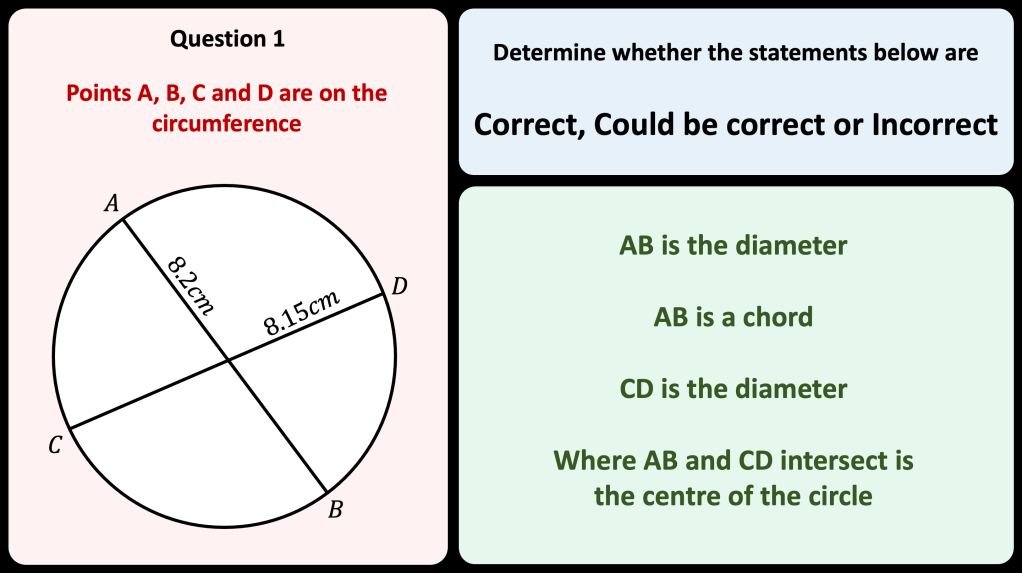
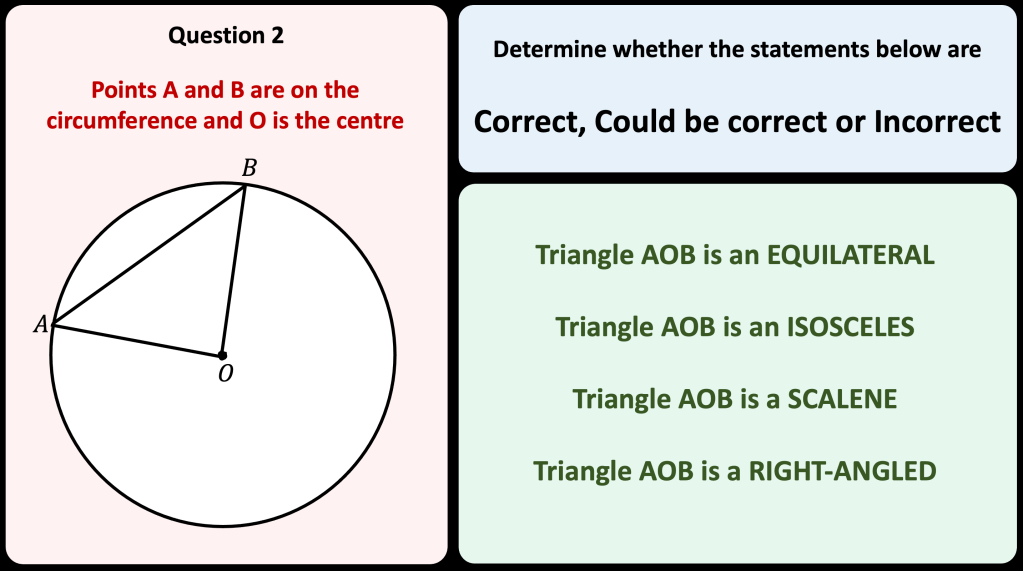
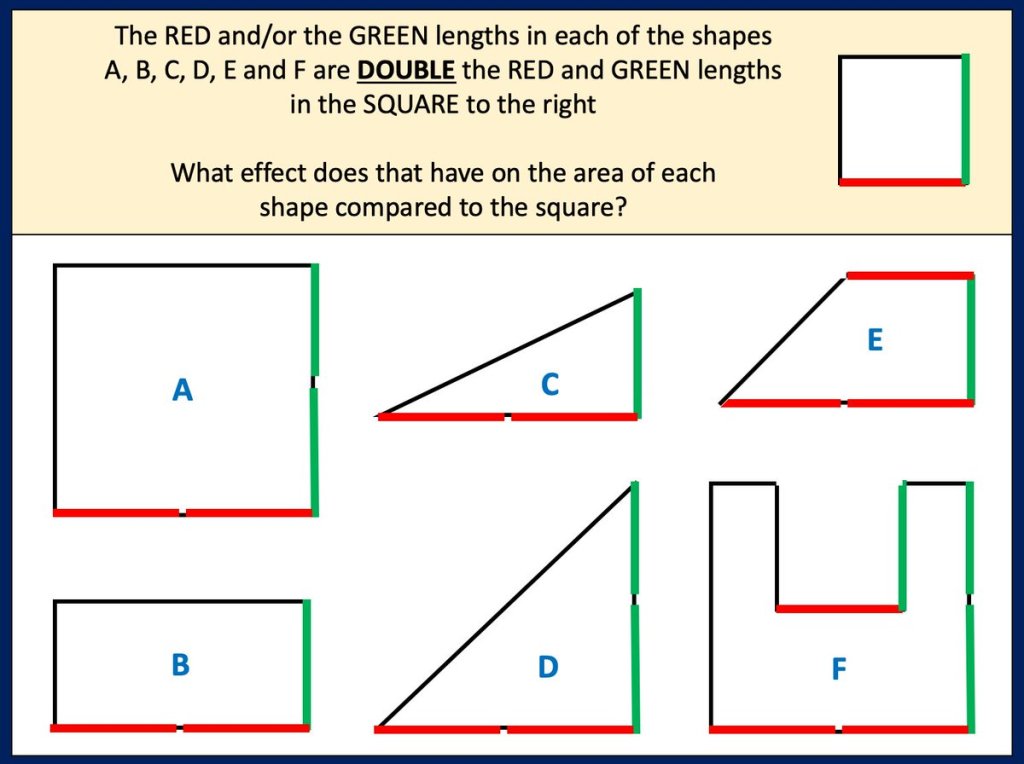
Area and Perimeter of shape problems
Perimeter and Area of Irregular Shapes
I have been looking ahead at some topics I will be teaching in the first term and one of those is inequalities. I wanted to look at some activities where students could identify shaded regions. I thought one activity could be to identify correct inequalities when the co-ordinates were substituted. Then once co-ordinates were identified as lying in a region I thought that then next step was to use this to find the correct inequality.
I have been playing a game called ‘Cheeky Monkeys’ with my daughter and the winner is the one that has the most bananas (the bananas are being held by the monkeys) I watched how my daughter lined them up in rows and then proceeded to count the bananas. I started counting the 1s and then the 2s and 3s so added 4 and 6 and 9 and made 19 but then considered the fact there was 3 rows of (0+1+2+3) and then an additional 1 too. This made me wonder about how we add up groups of numbers that have repeated rows Empty Boxes
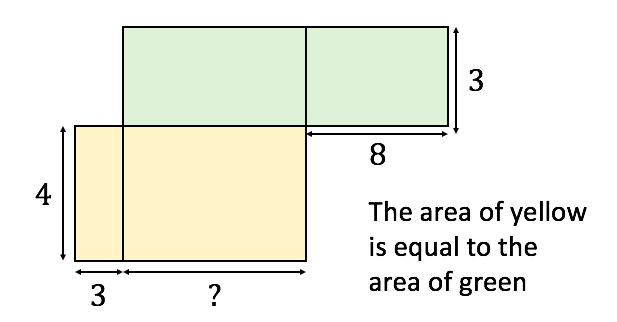
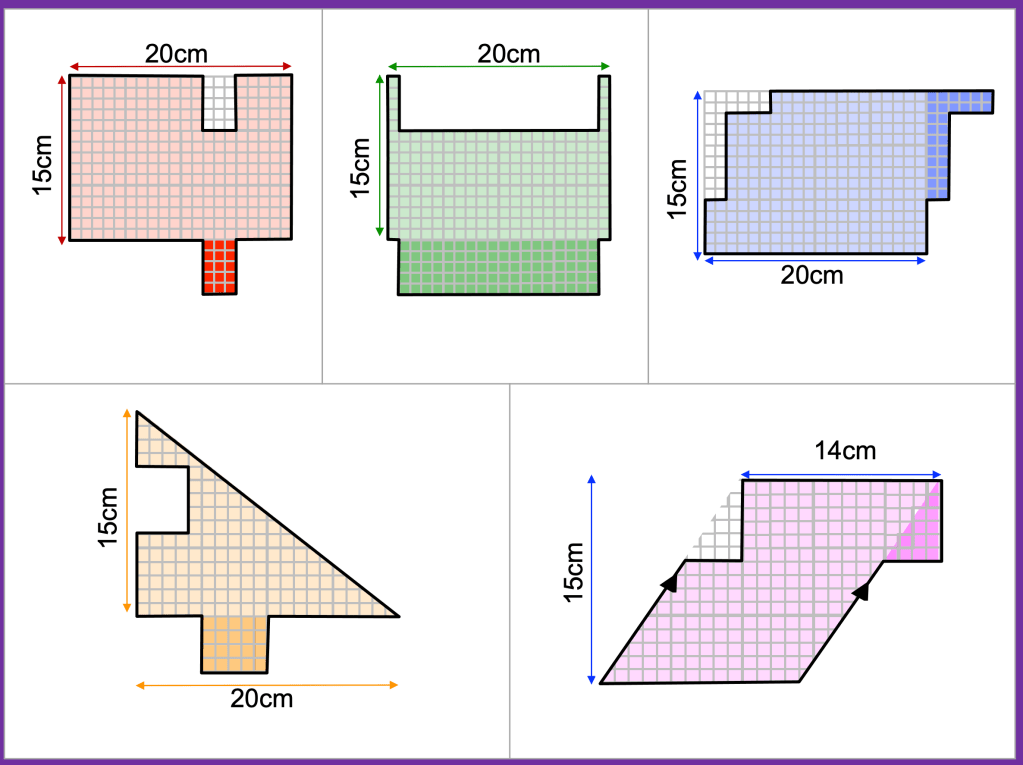
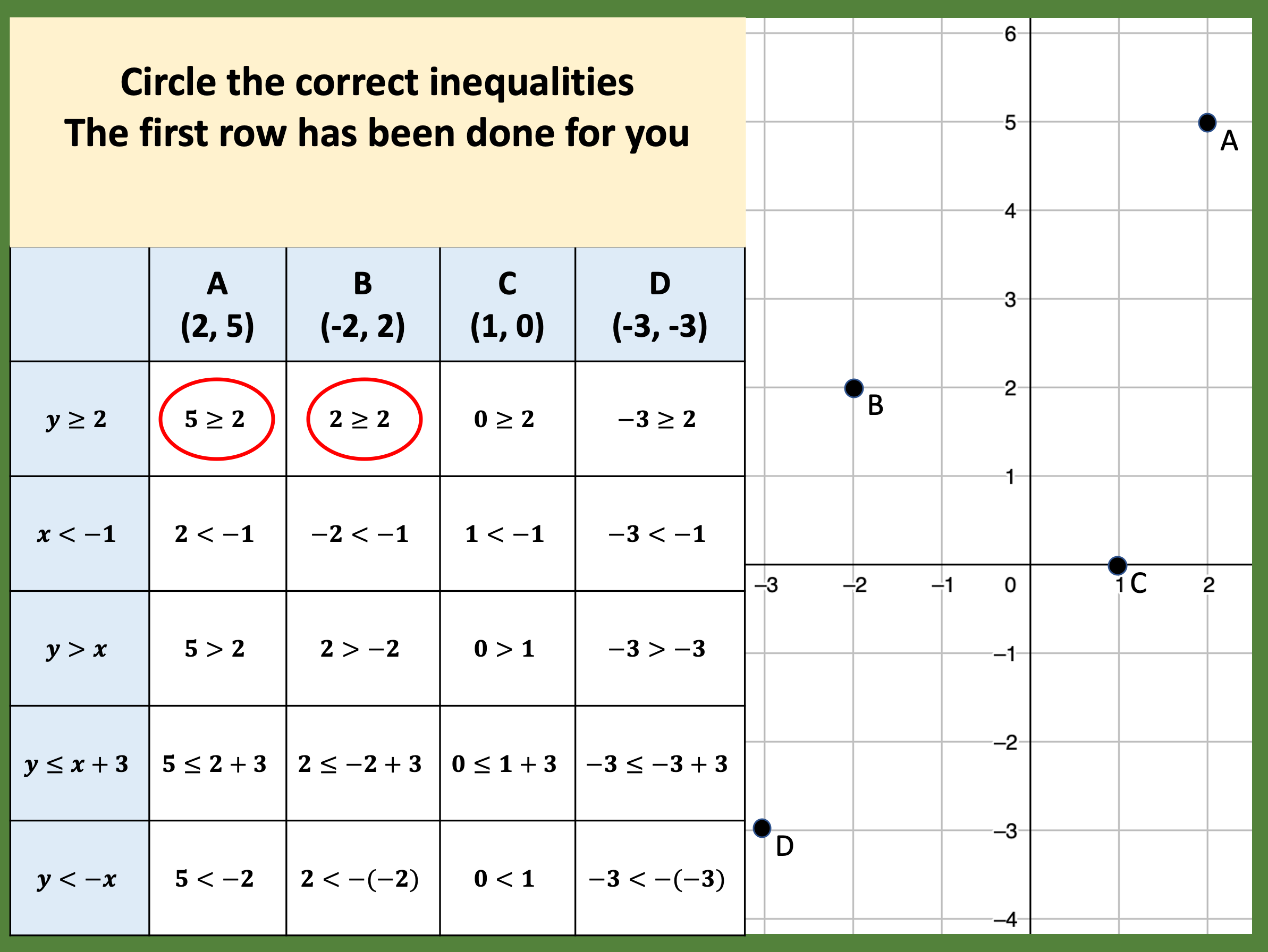
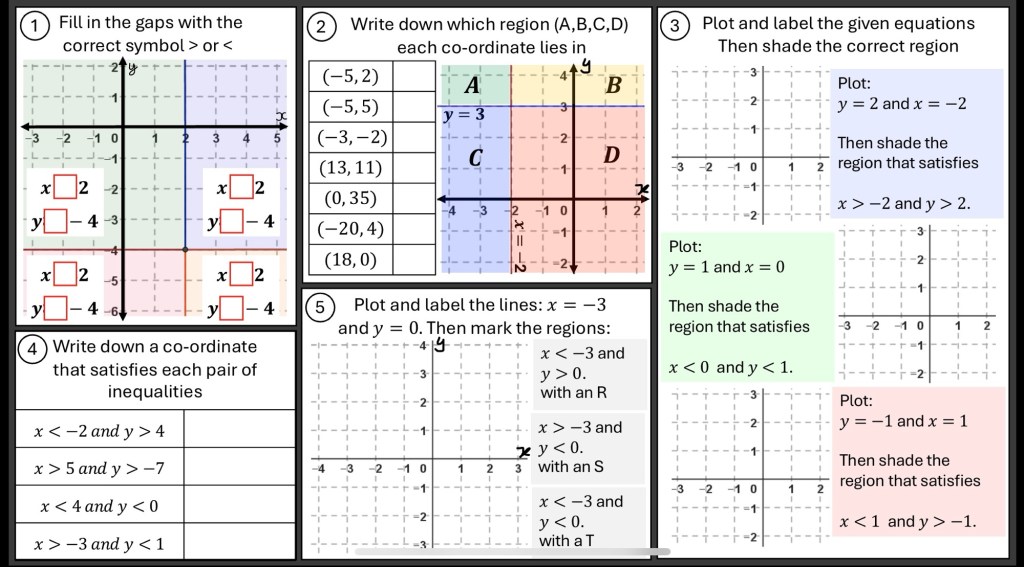
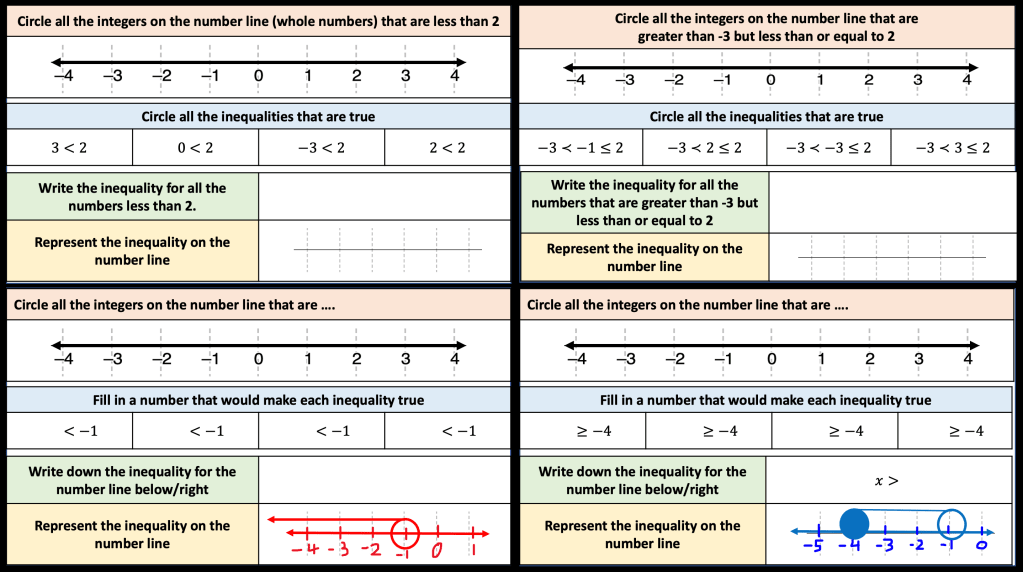
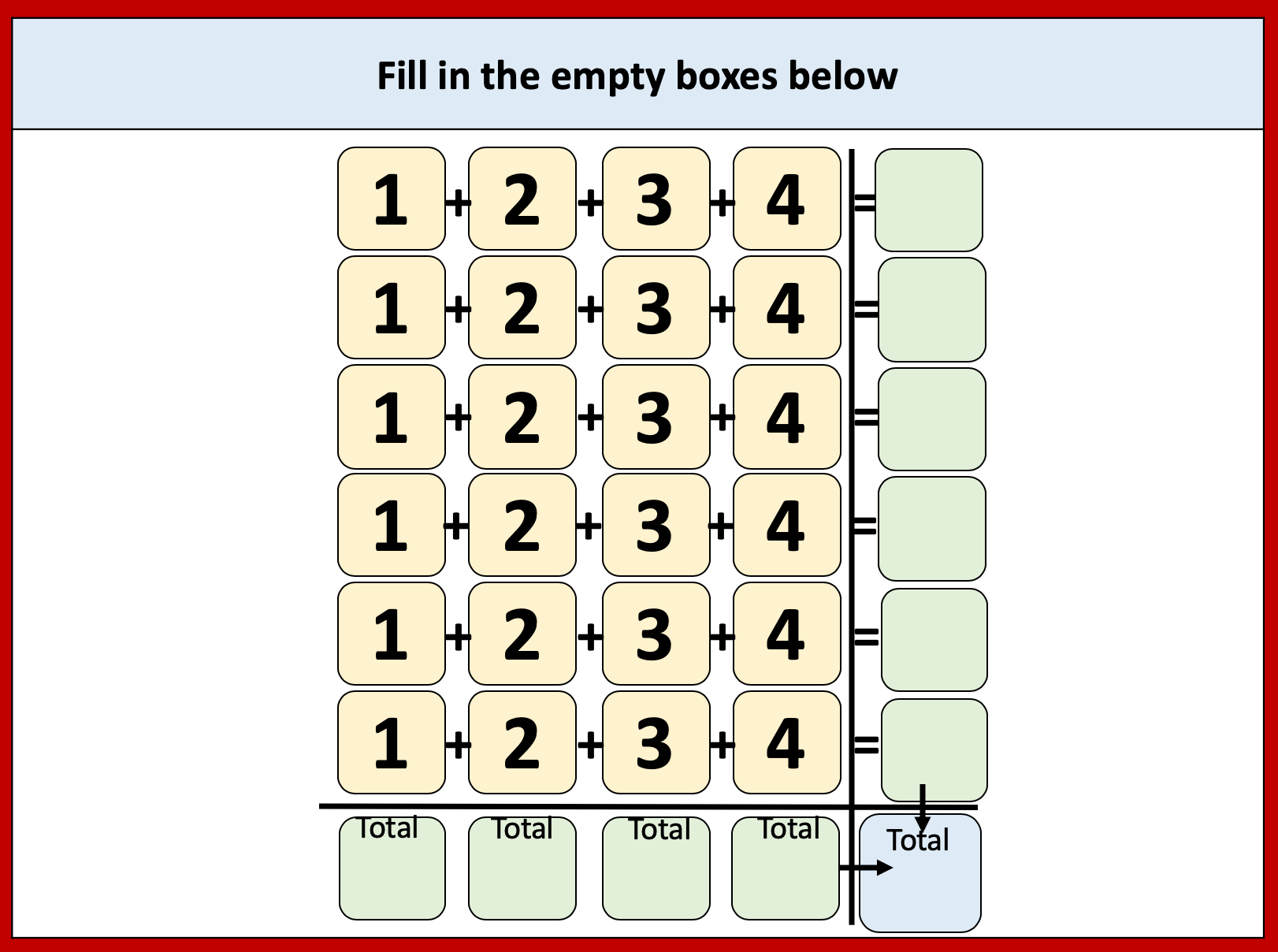
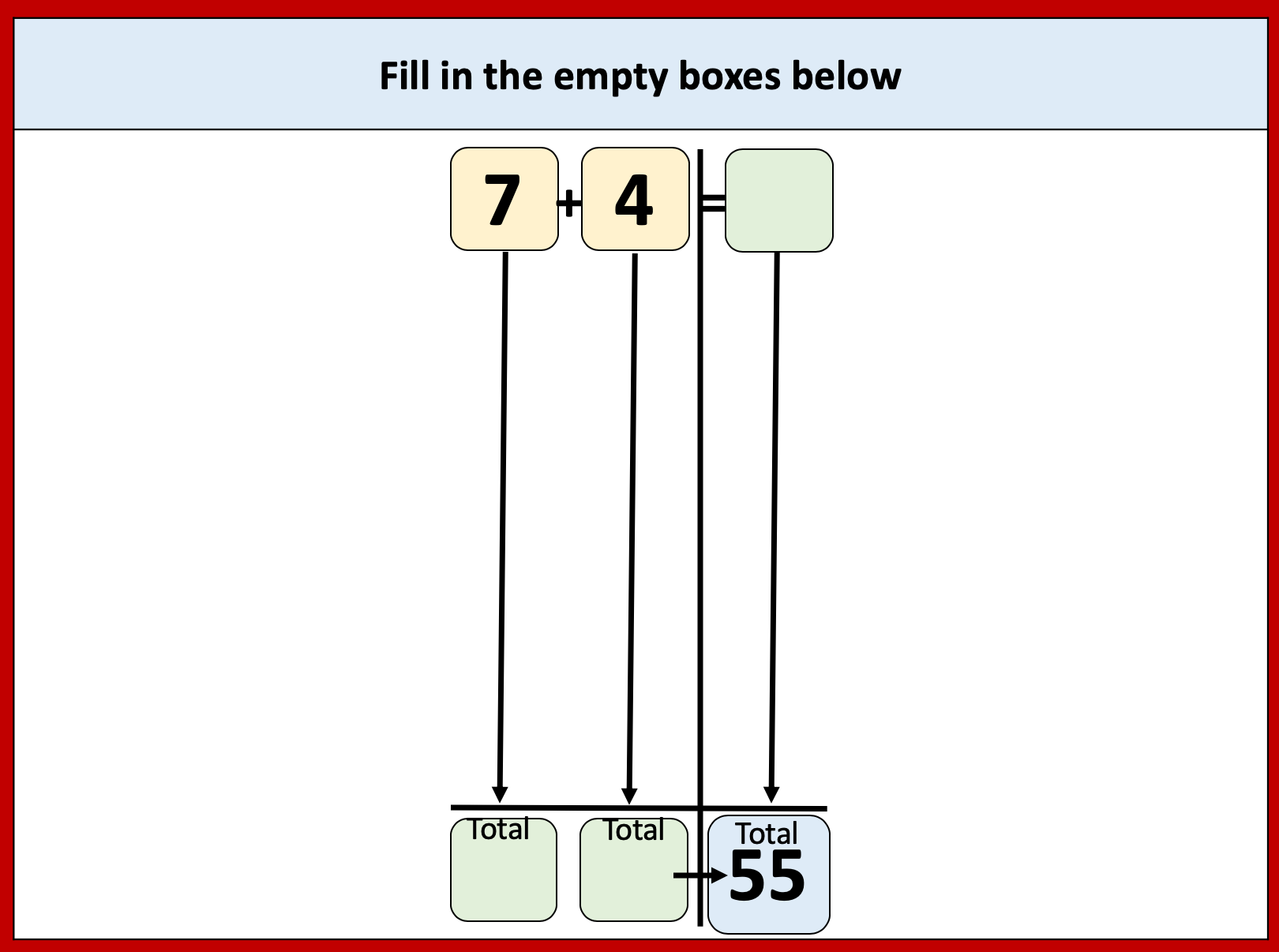
I was thinking adding up numbers like these and at first I wanted to group the 8s but then thought that 8+7+3+2 was 20 and then it was just 20 times 6. I often like to check this by doing 48+42+18+12. So I thought it might be a good activity to try with my year 7 class in September. There are lots of ways I could extend it too.
I have looked at some variations of this idea
At the school I work at, we have a lot of shared classes because we are a split site school. We often have classes once a week and the other teacher has the class 3 times a week. At KS3, it was decided last year that the once-a-week teacher should work on numeracy skills. I have been playing around with some numeracy resources I wanted to try out with my once-a-week classes based mostly around the Distributive and Associative Laws.
It’s funny that sometimes the most straightforward ideas can sometimes be quite surprising (for me anyway) The latest such idea is that the circumference of a circle with diameter 8cm is equal to the length of an arc of a semicircle with diameter of 16cm. I know this to be true but it just surprises me every time I see it.
I’ve added in the slide with AREA of semicircles too but just so students can see that area is affected differently to perimeter when scaling the diameter.
Looking forward to September and I have seen that I will be teaching Circle Theorems in the first term. Its not a topic I’ve taught in a while so I wanted to have a look at some issues that I think may arise (if memory serves me well, students sometimes incorrectly identified some theorems because they ‘looked’ similar to others) so I wanted to create a few resources, that I could use if needed, that hopefully highlighted these errors that students made.
I decided I’d start with finding missing angles in triangles where two sides are the radii of the circle. We’ve been looking at area of sectors and circles in the previous lesson so they have been exposed to some of the terminology needed. Then after looking at angles in a triangle I would like to look at angles subtended from an arc from the centre… then work my way through angle subtended from an arc at the circumference… and then angles in the same segment. This will be plenty for one lesson and all are linked. The second lesson I’d look at a few more. I want to use questions to build up the ideas after we discuss them and then spend lessons looking at more complex problems.
A simple 10 question build up of some of the circle theorems. Students liked using this as a practice starter.
I have looked ahead at the SOW and seen its time to teach Circle Theorems after HT. I want to make sure of a few things. 1.) students really understand each theorem properly and not superficially. So by that I mean, if they see a diameter drawn they know the angle subtended from the diameter and touches the circumference is 90 degrees but equally that if and angle is marked as 90 degrees that the chord its subtended from is a diameter. I also want to interleave other topics with circle theorems that solidify students understanding angle geometry such as similarity and angles in parallel line. The task below requires no knowledge of circle theorems, I wrote it a while back for year 8s looking at angles in triangles. However I am going to use it with year 10 to reinforce the idea that the radius is equal length wherever it drawn on the circle (centre to circumference) and it creates an isosceles triangle.
Question 1 is a reminder that given two chords, if one is definitely the diameter then that has to be the longest.
I wanted a series of questions that looked at the effect of double the base number whilst squaring. It makes me think of when we double the lengths of a 2D shape to create similar shapes but the area is 4 times as big. I wanted to look at the idea in this way as a precursor to looking at area and volume.
MathsHKO 