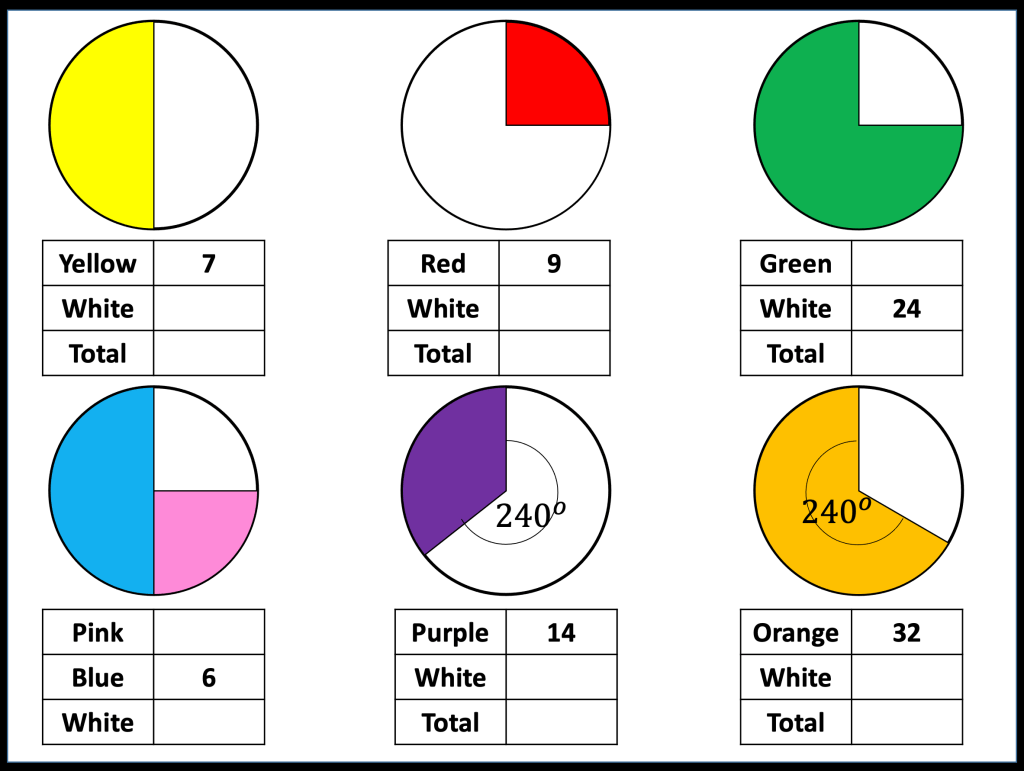
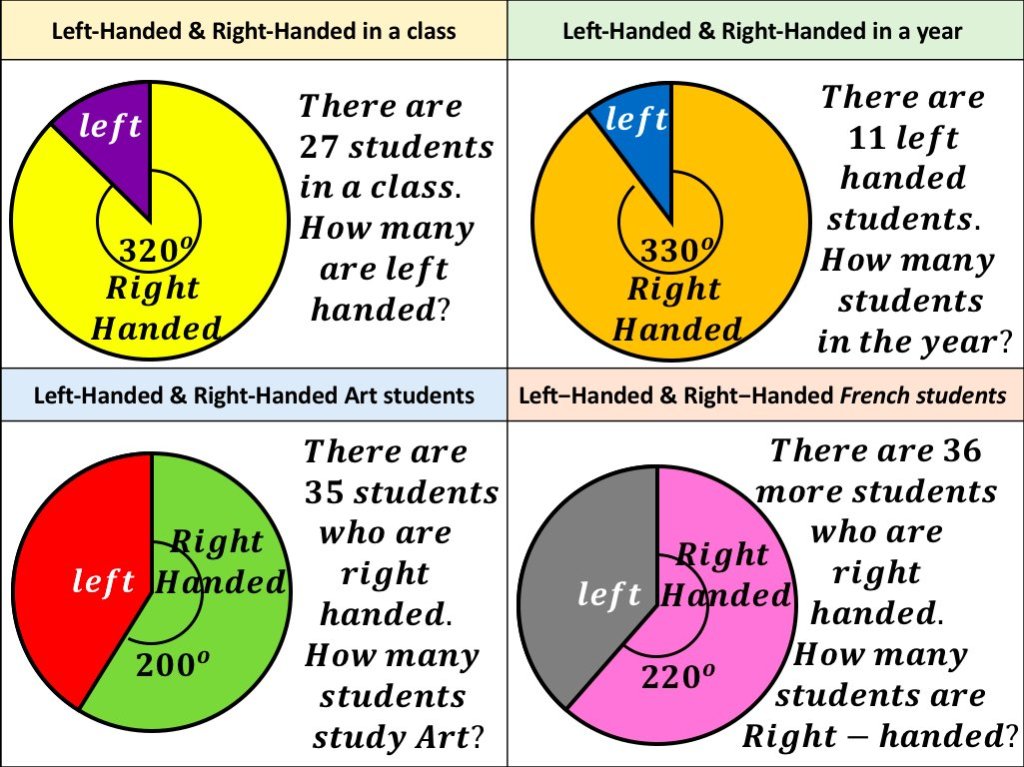
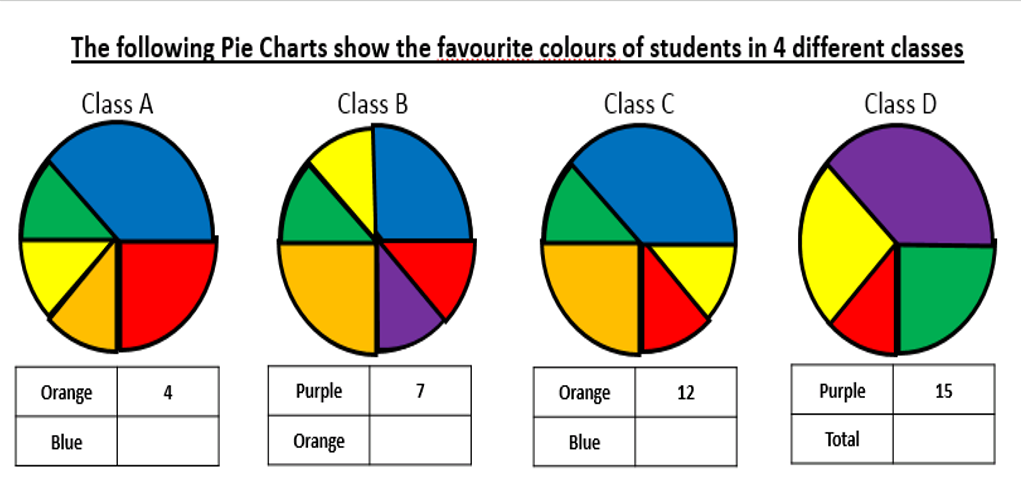
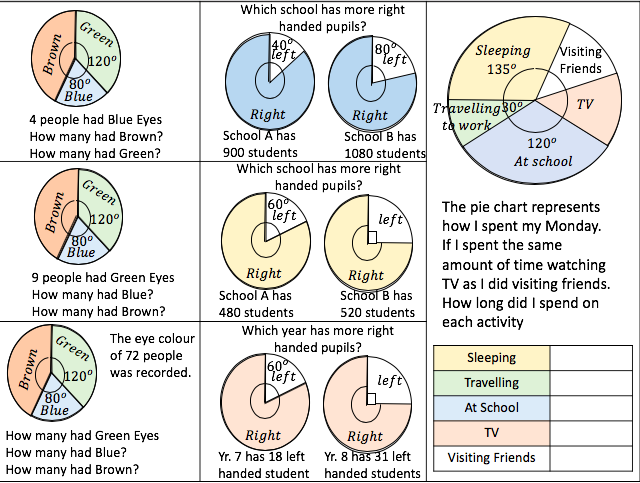
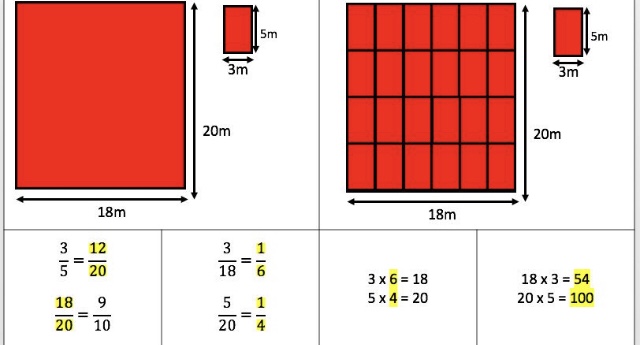
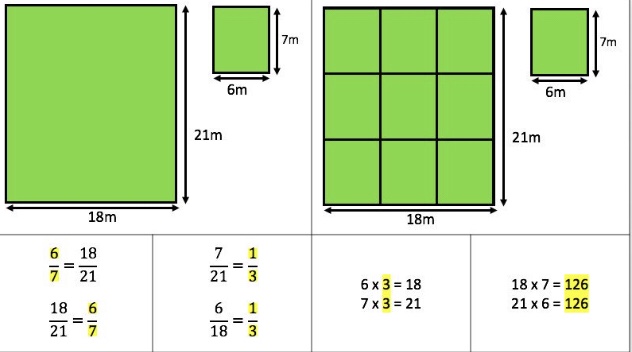
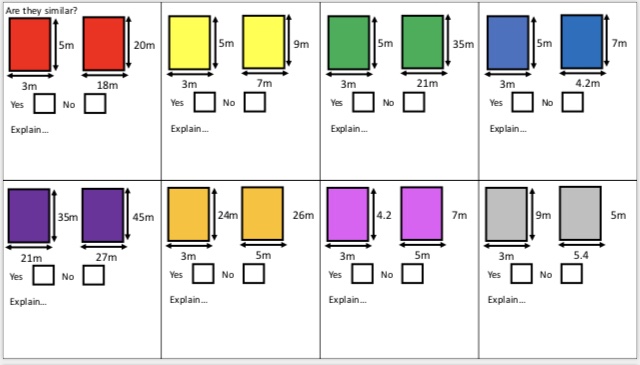
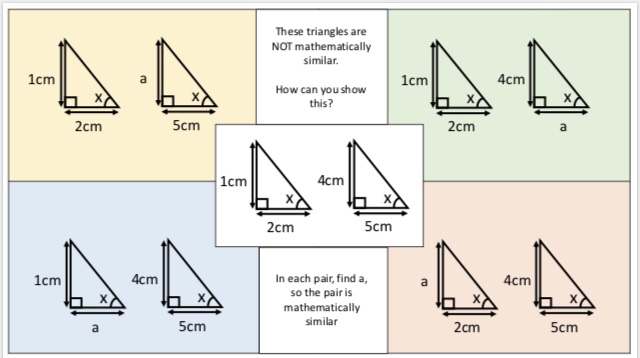
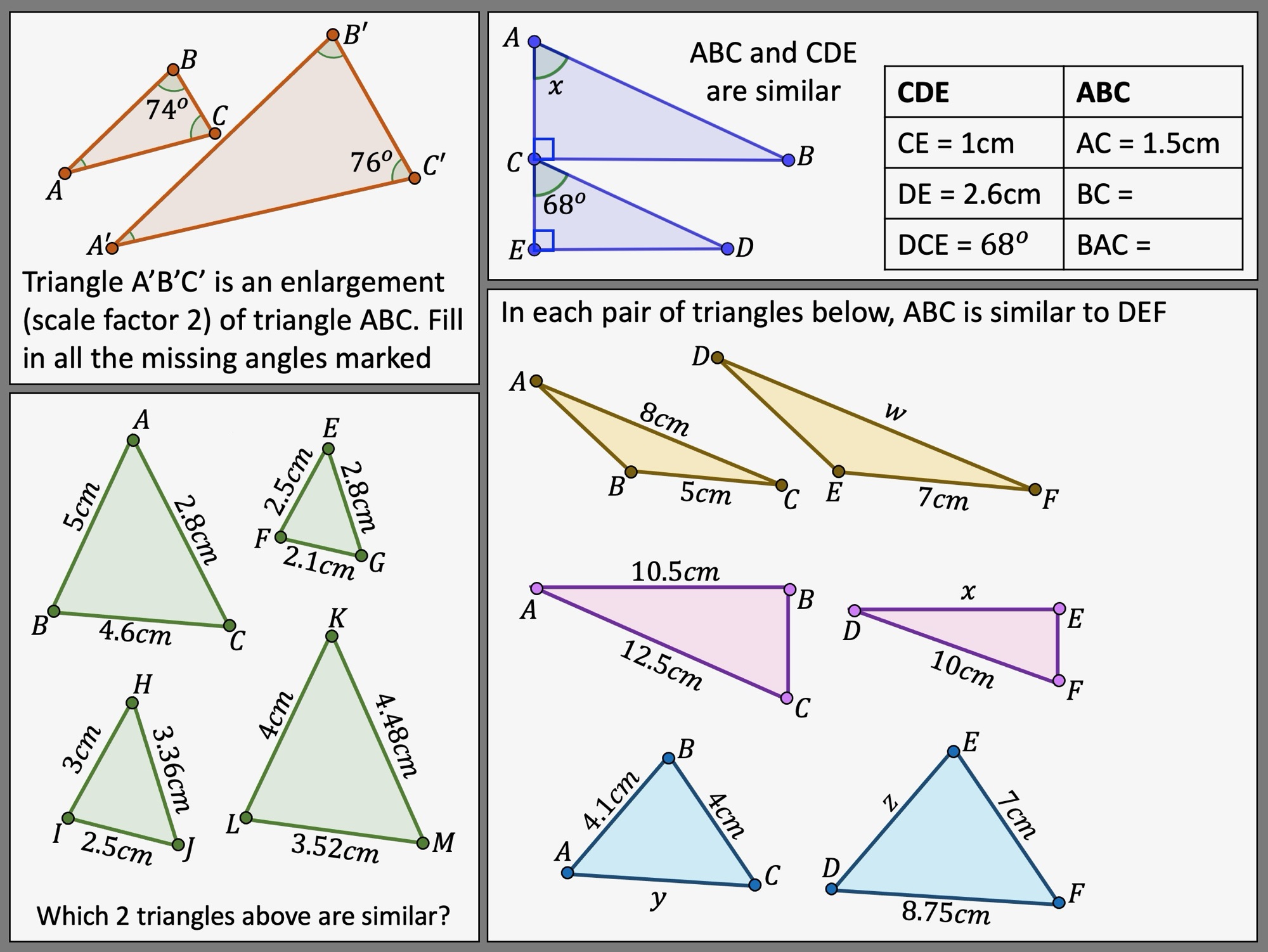
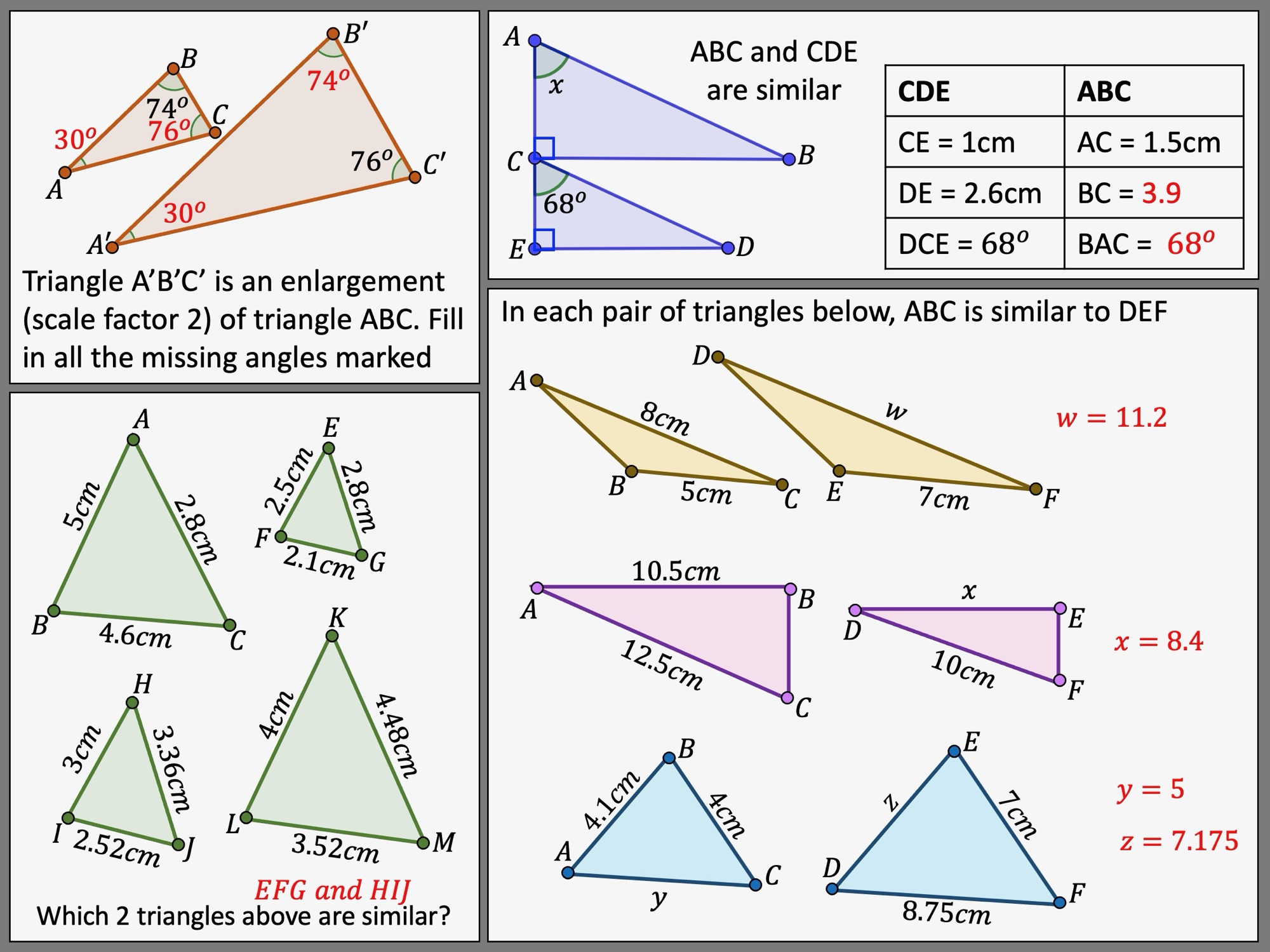
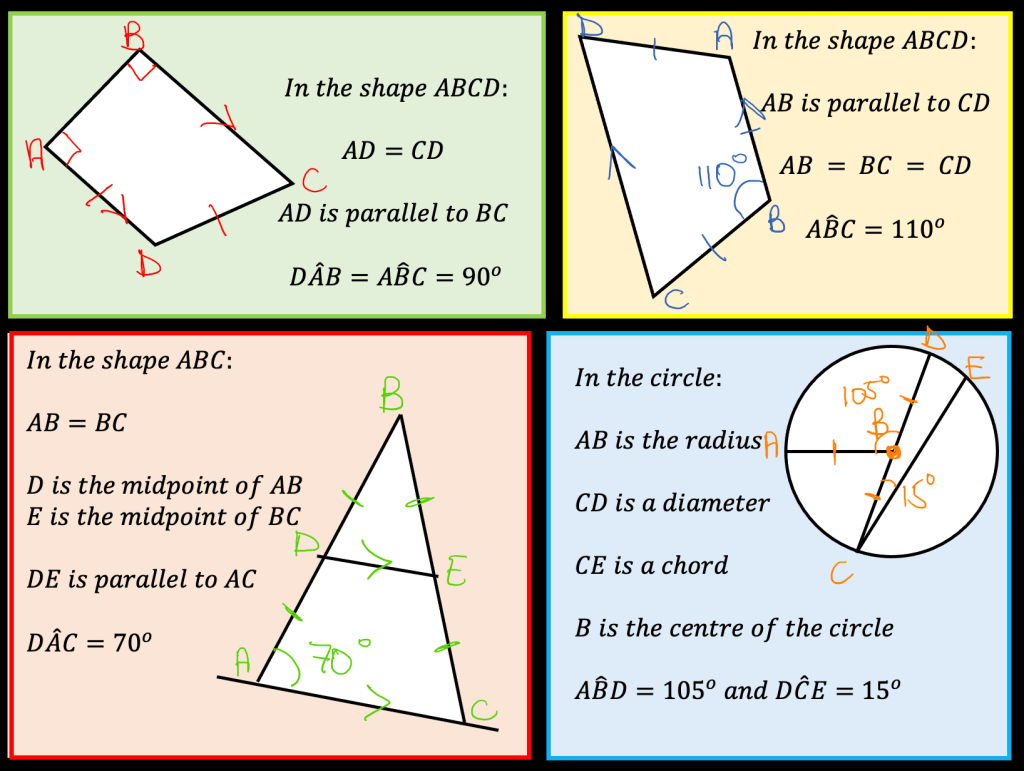
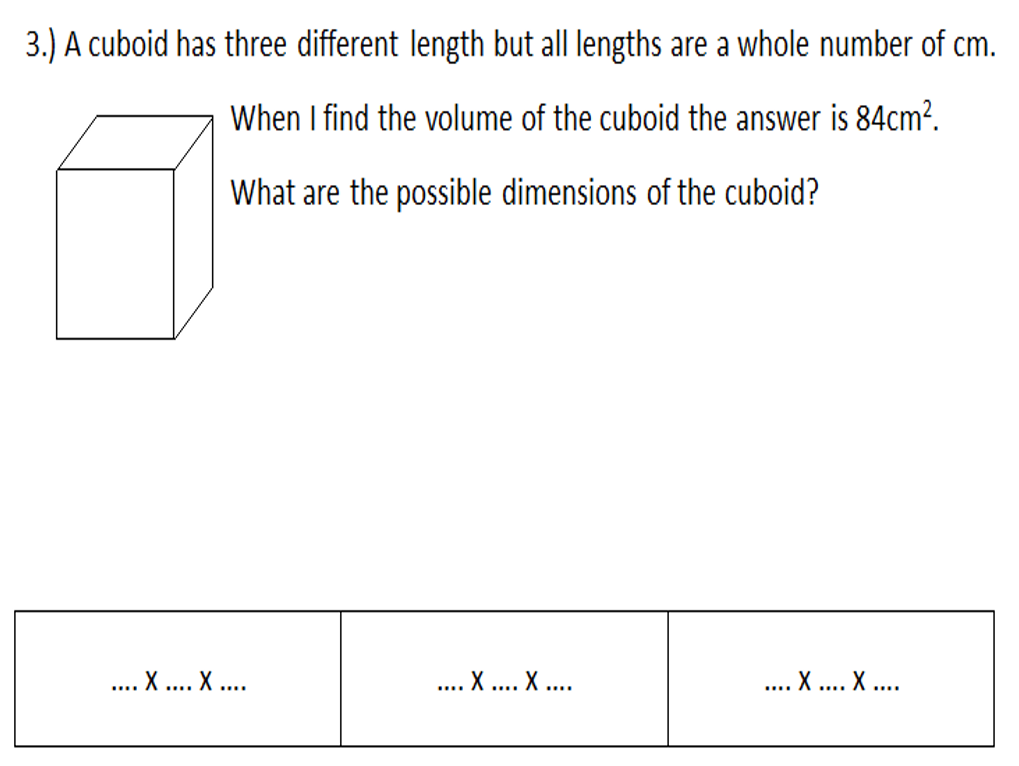
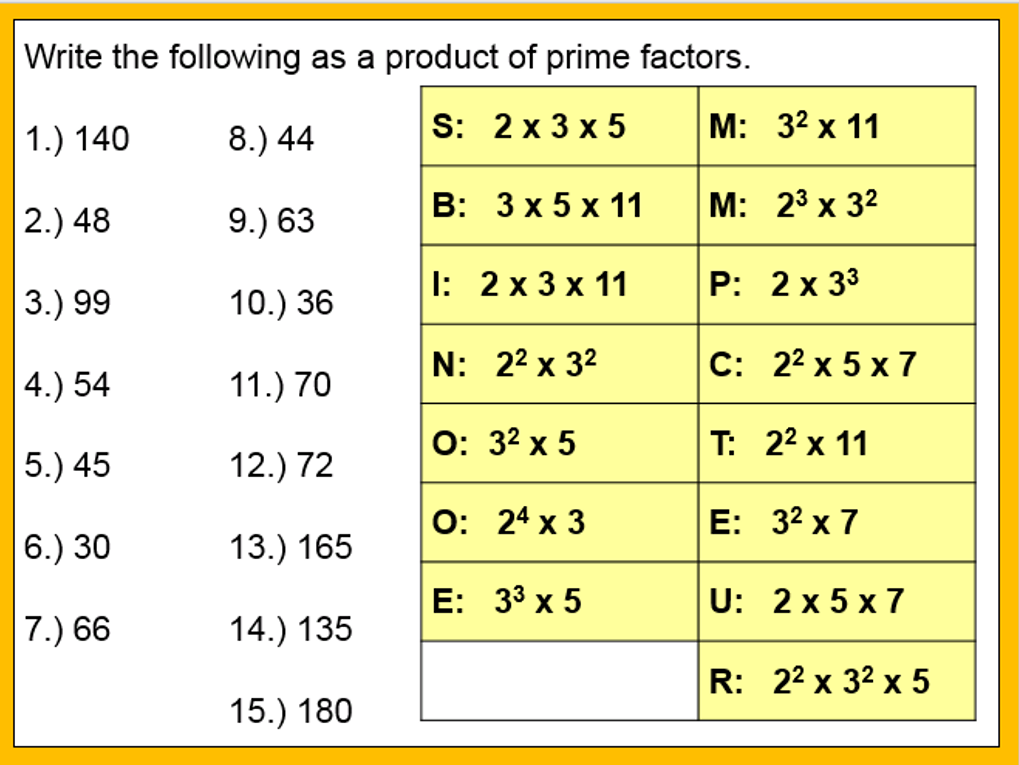
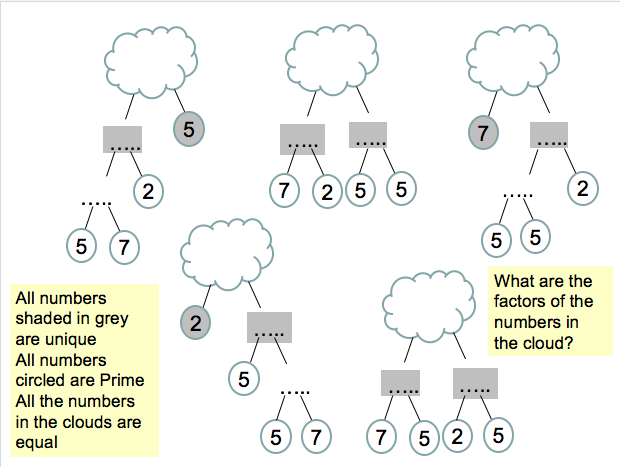
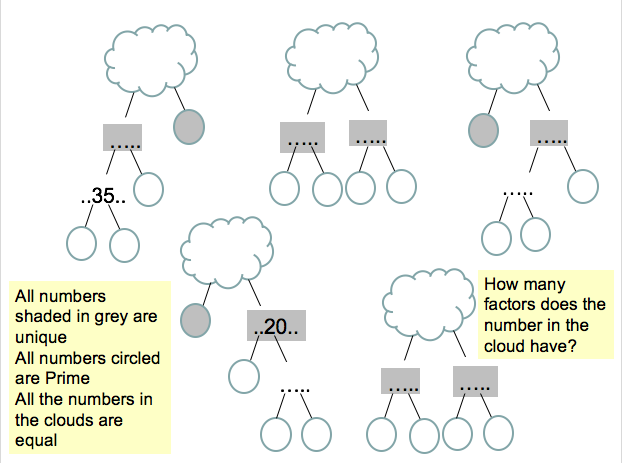
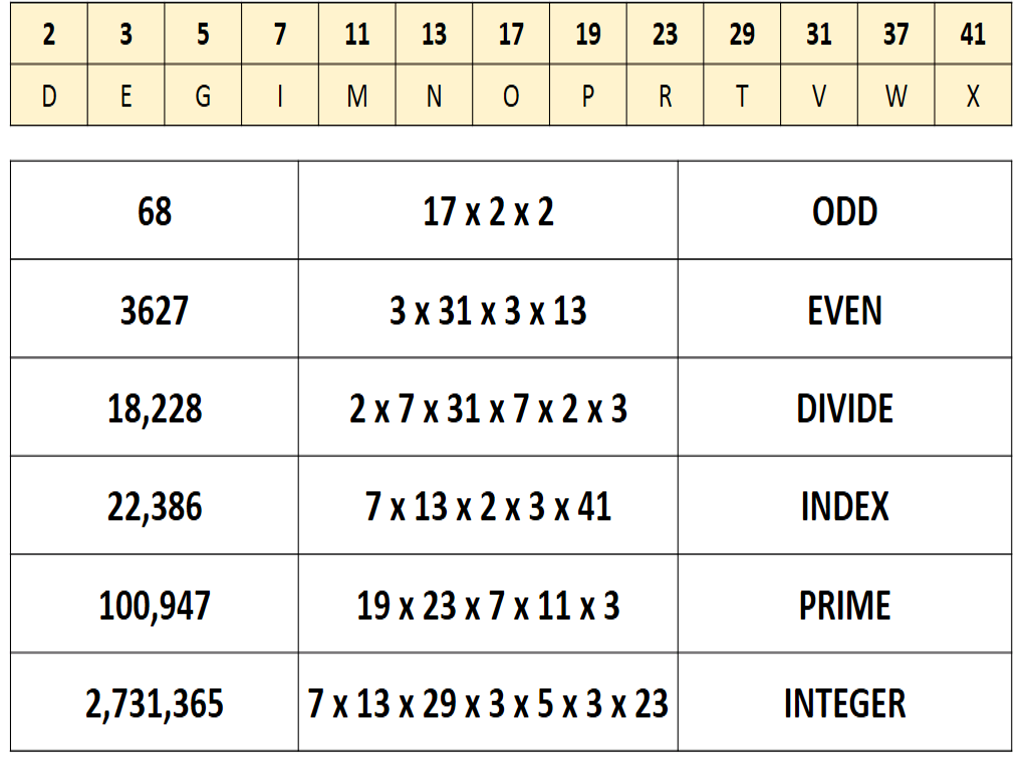
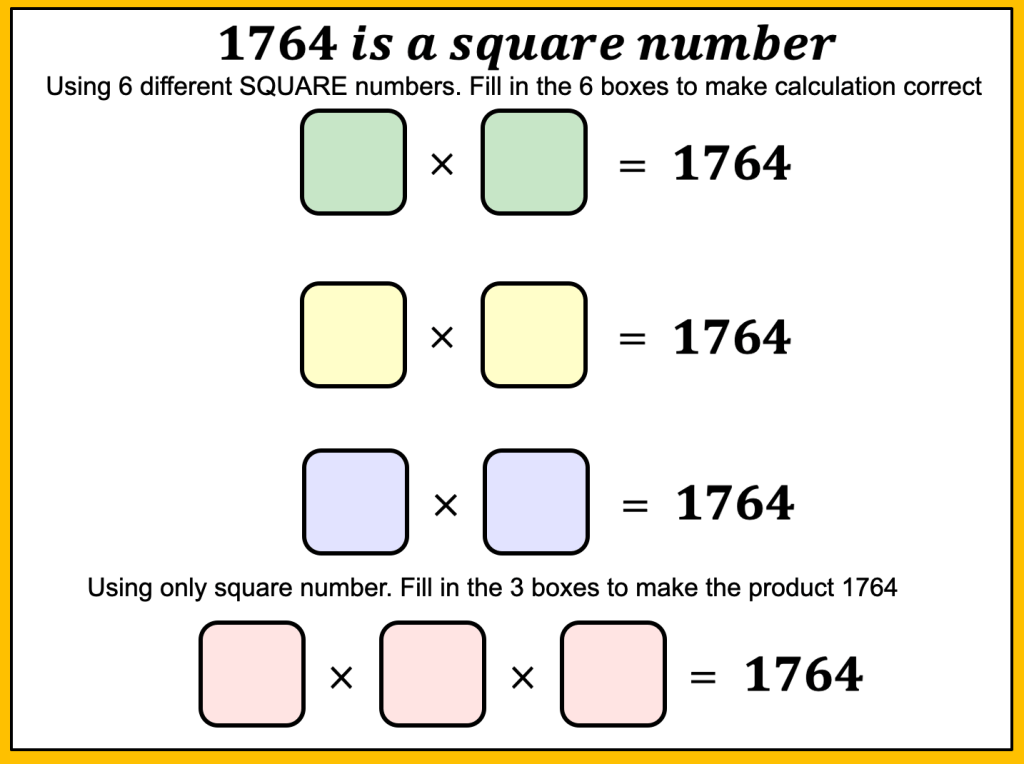
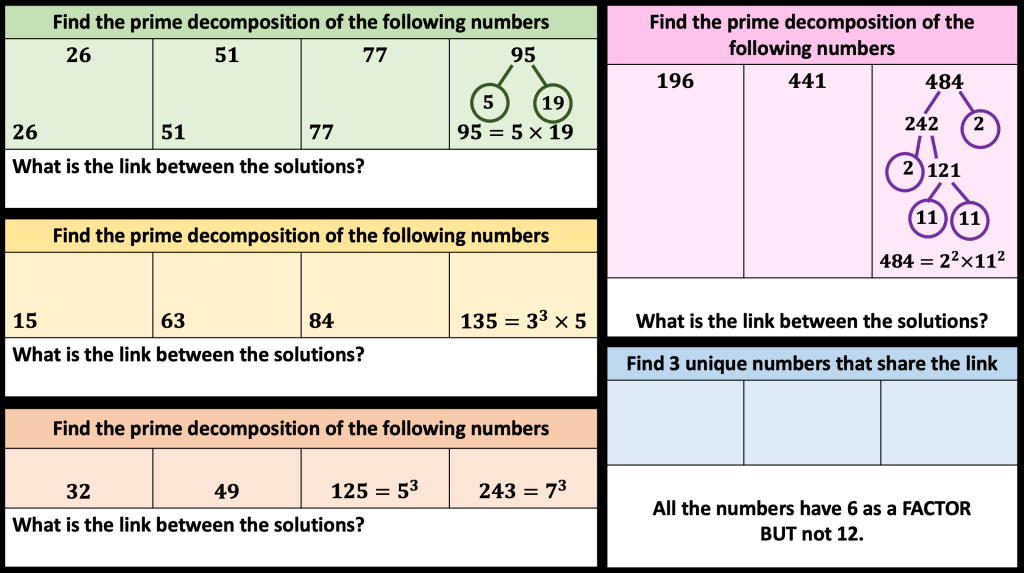
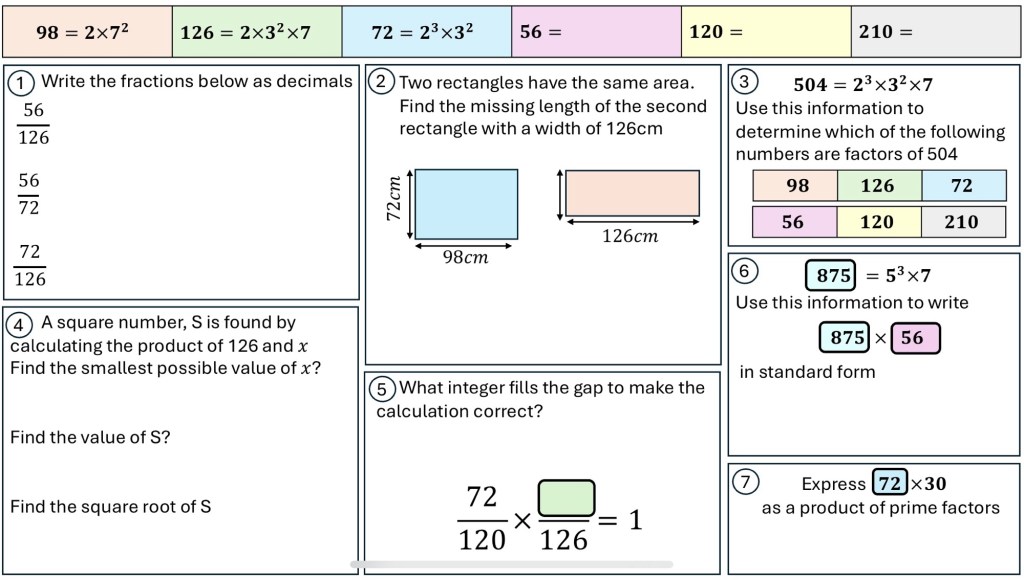
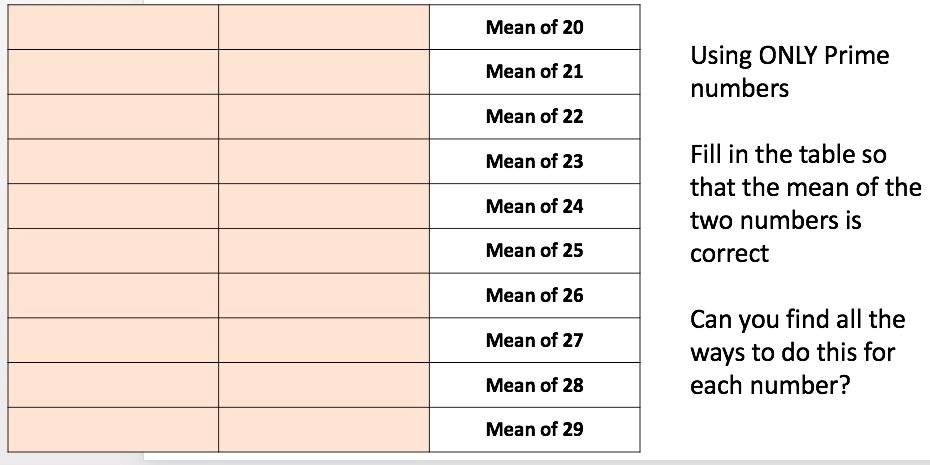
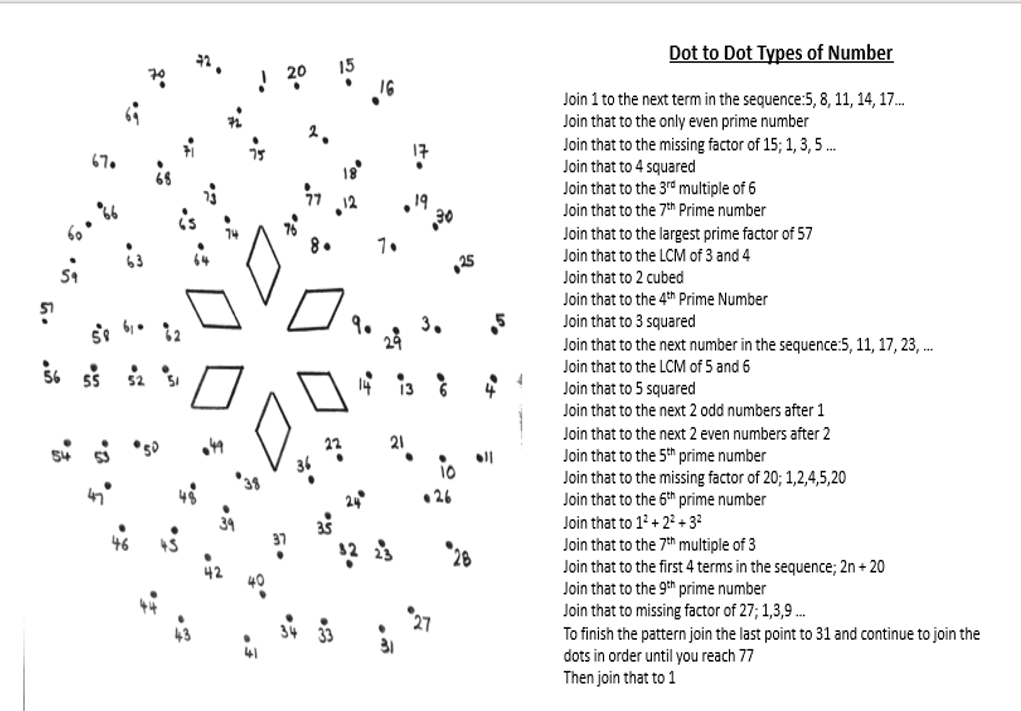
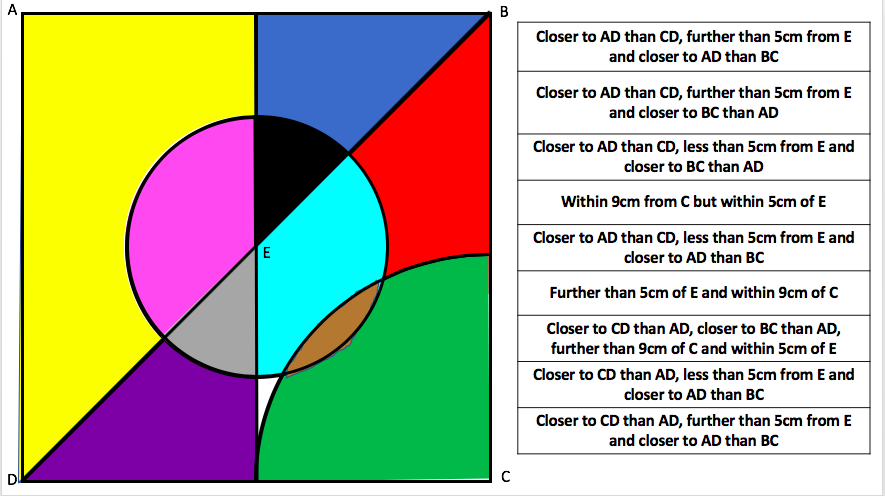
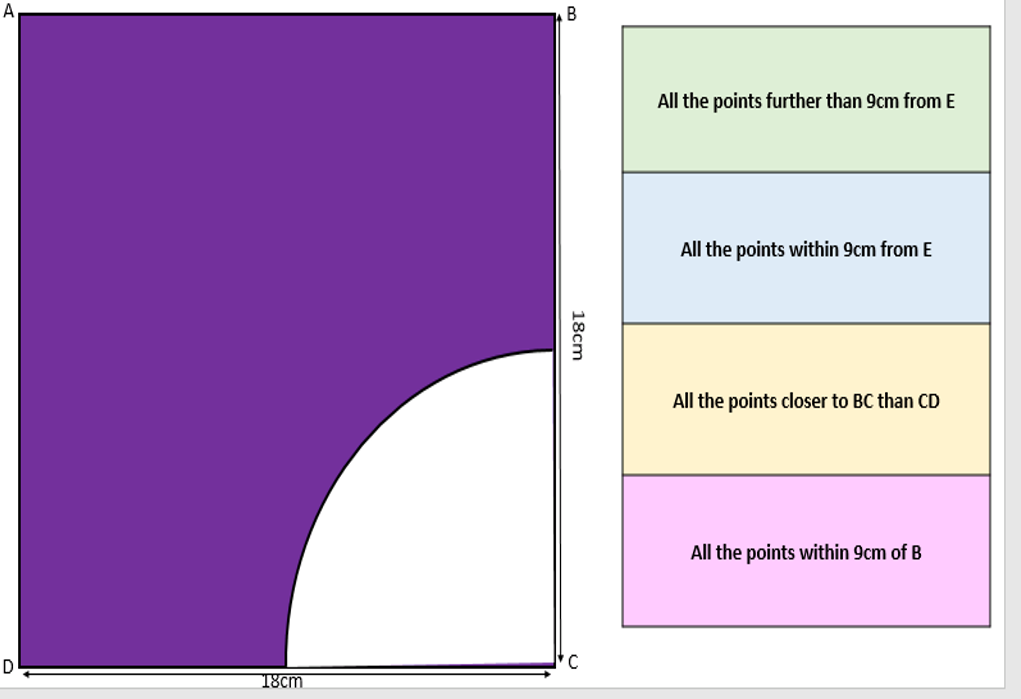
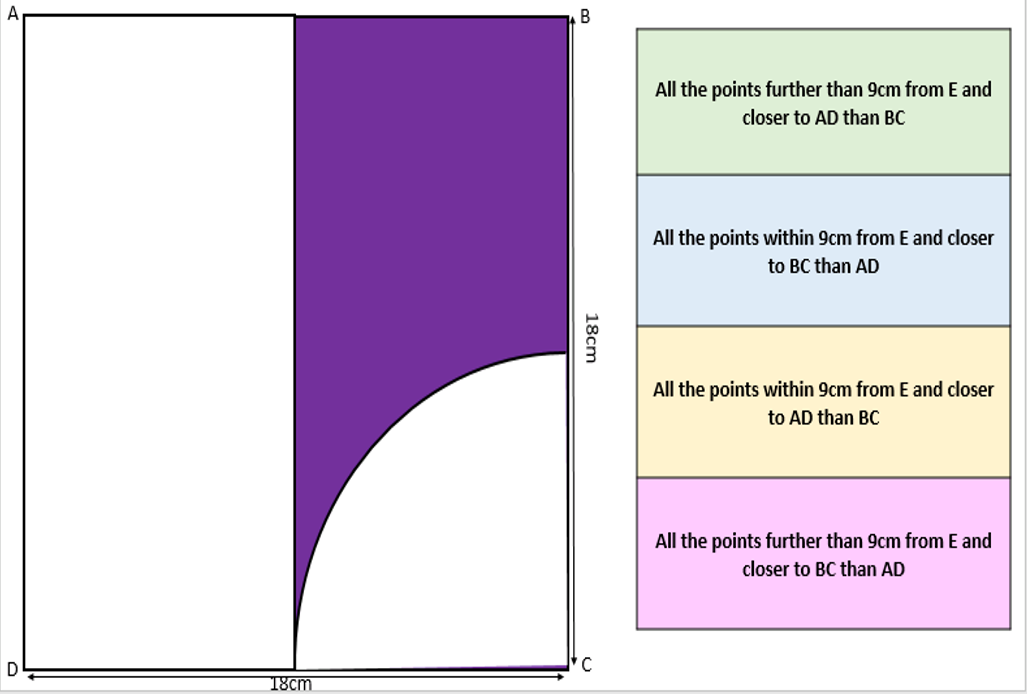
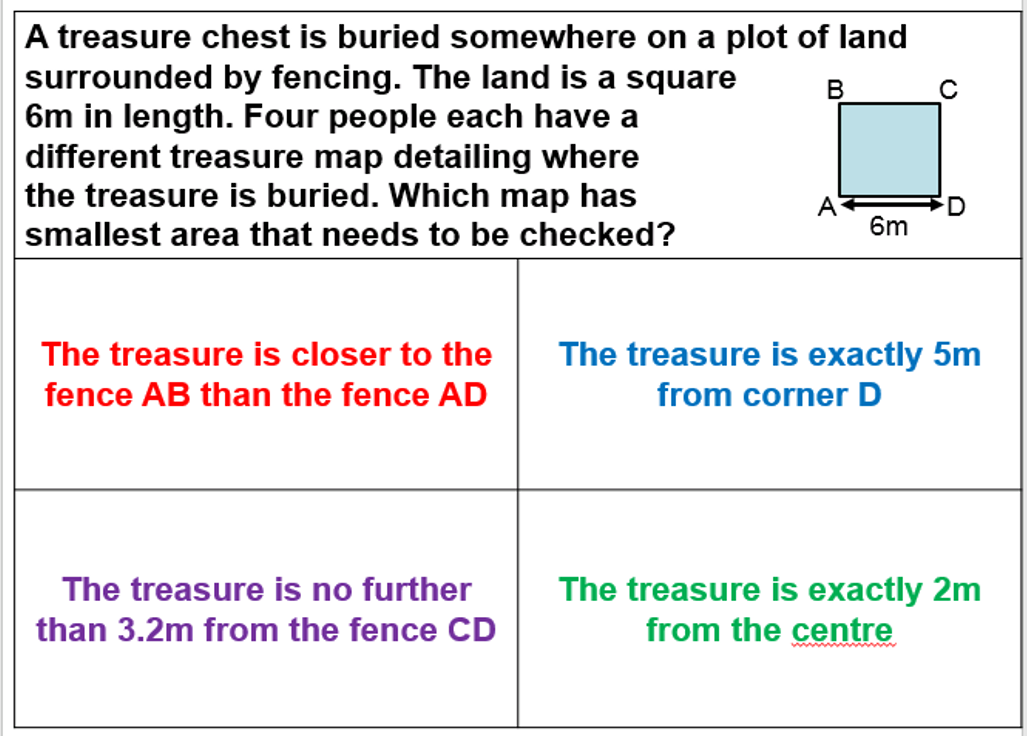
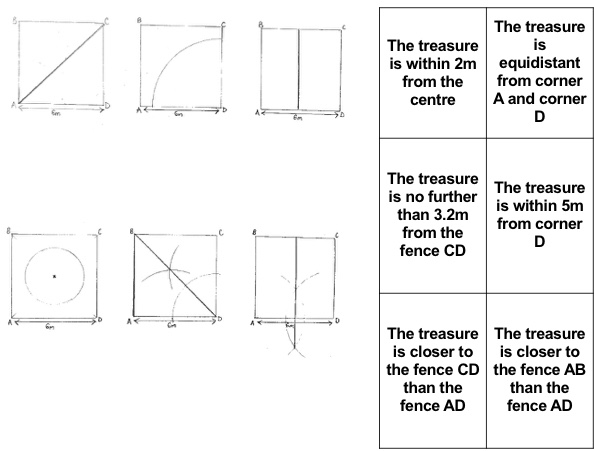
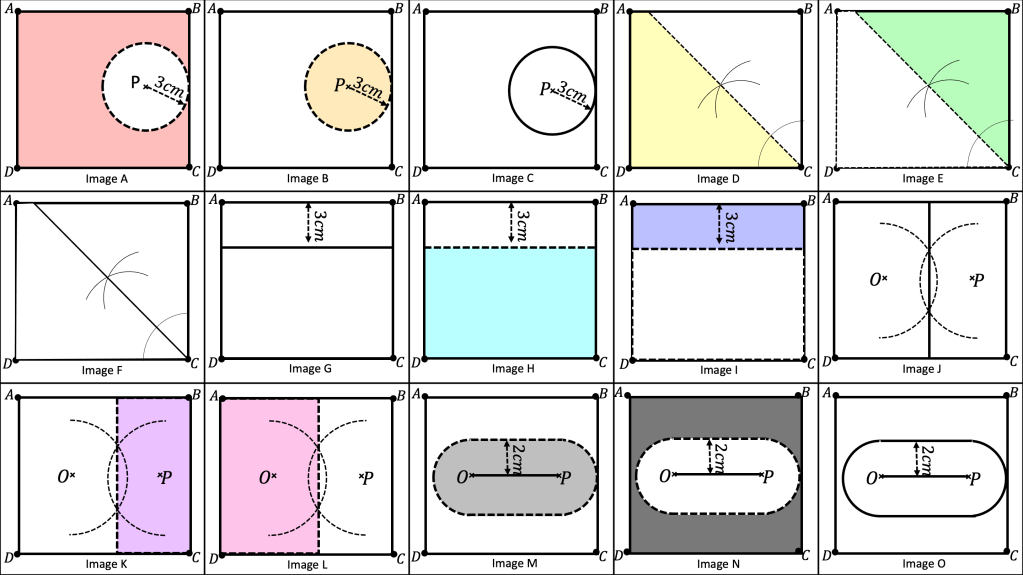
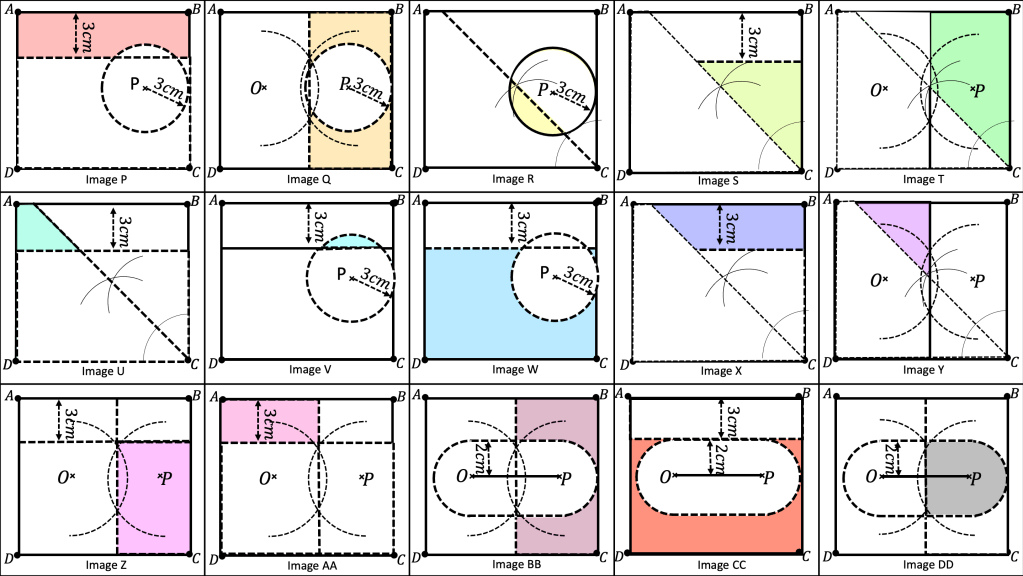
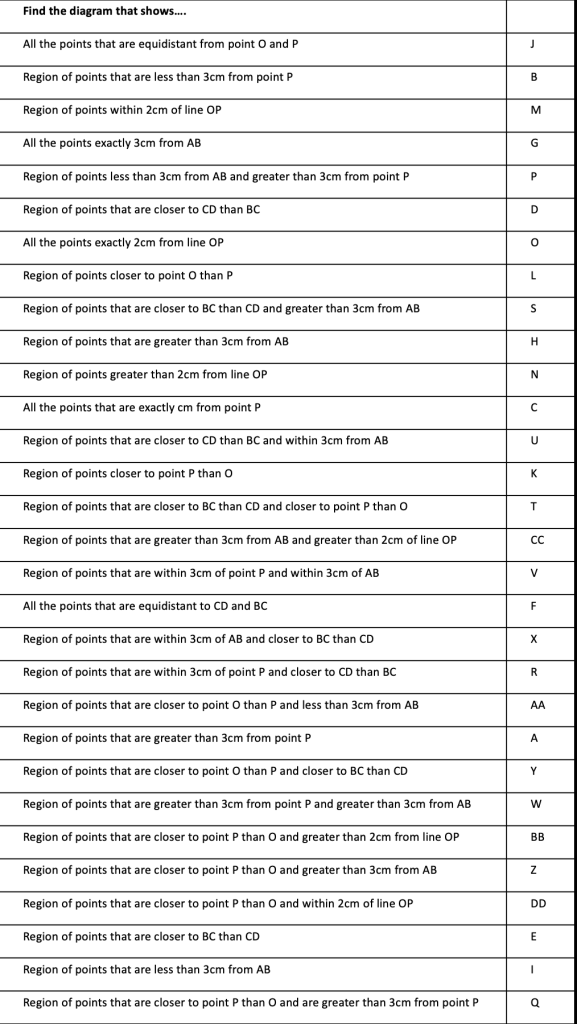
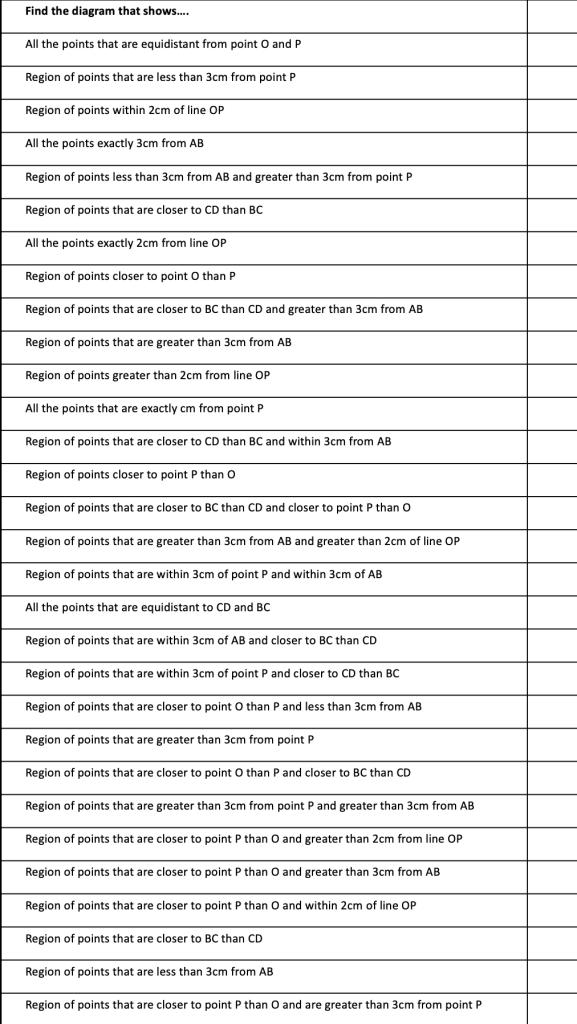
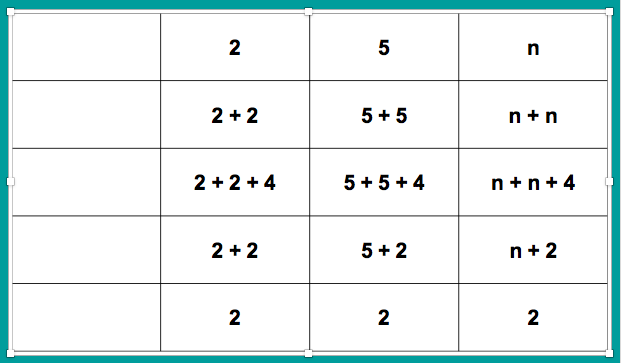
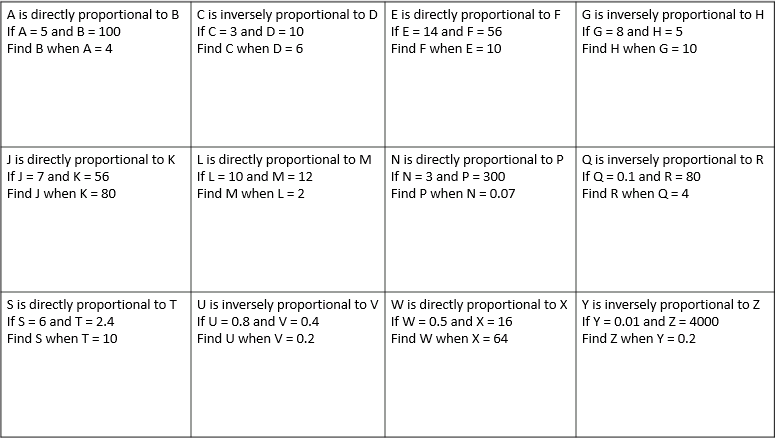
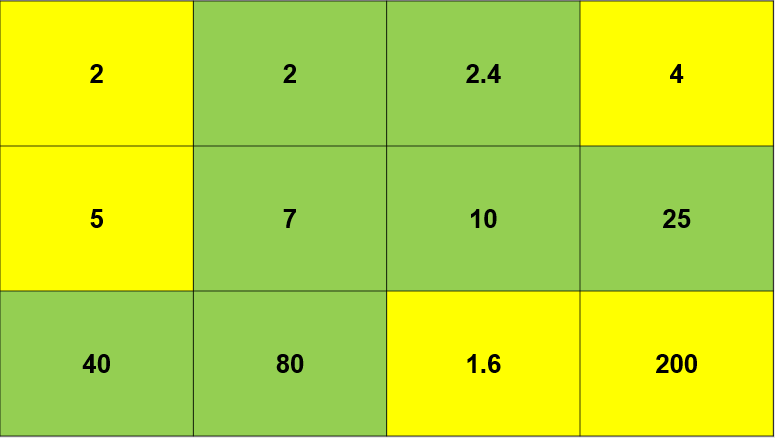
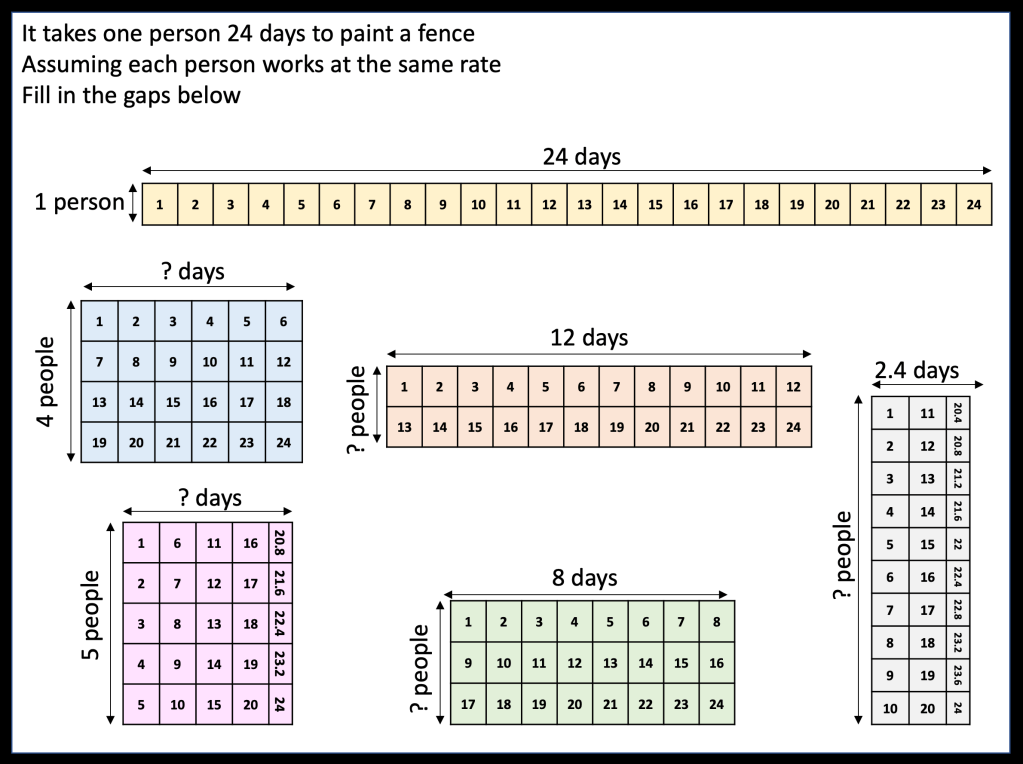
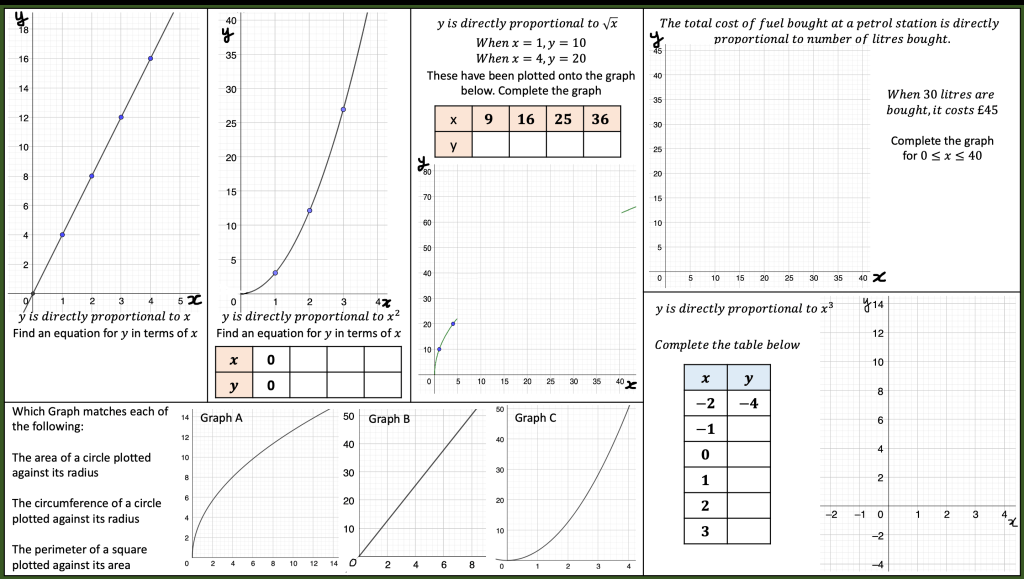
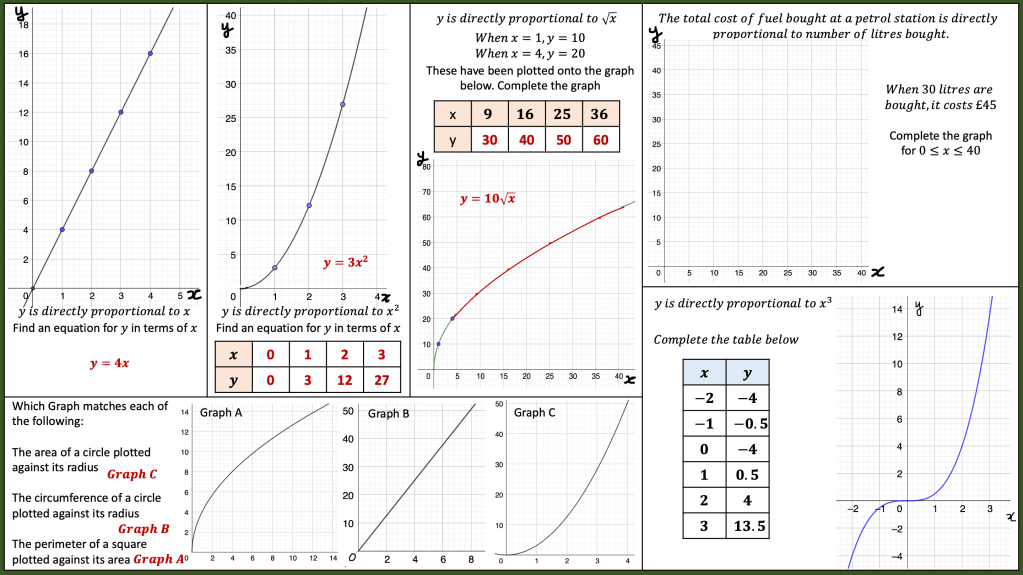
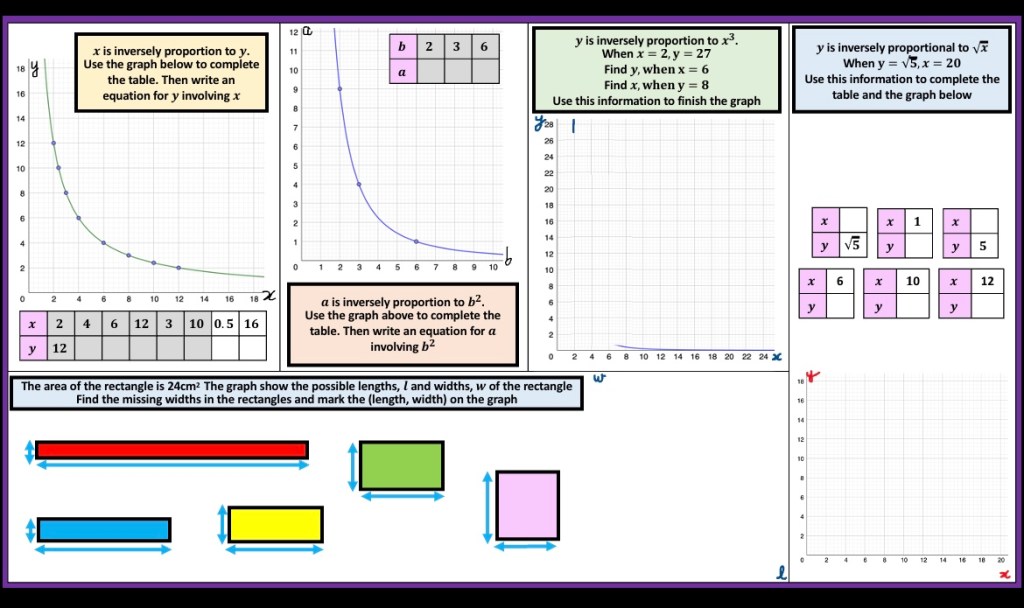
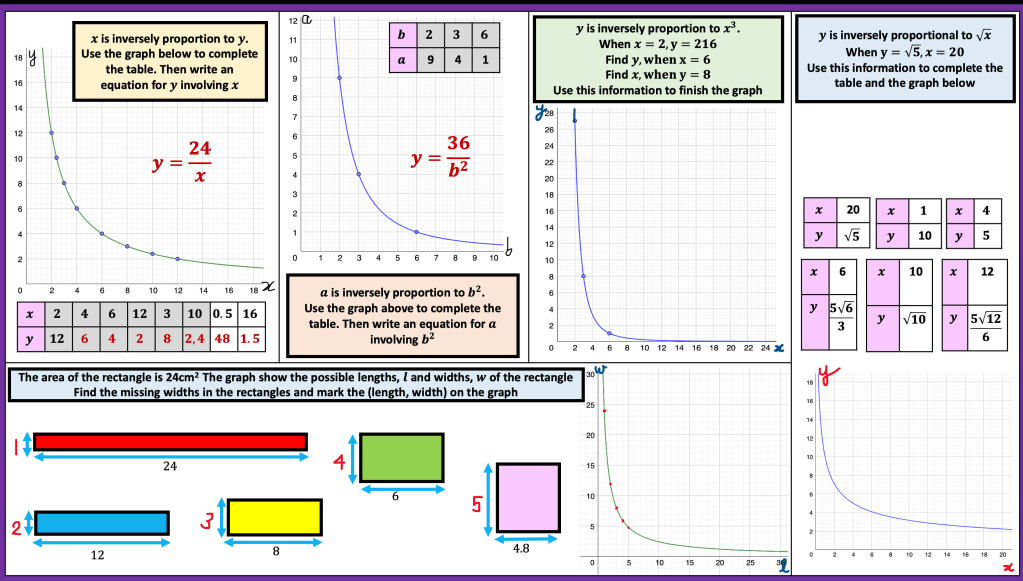
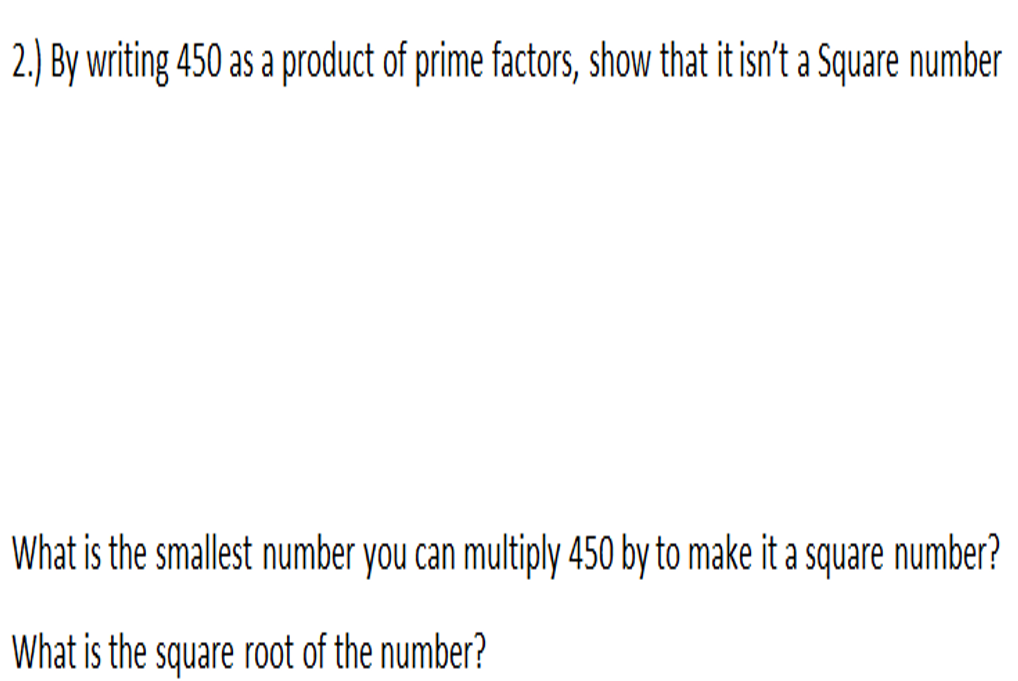I am about to teach Pie Charts to year 9 and have decided to look at reading and interpreting them first. I want them to understand that the slice of the pie is proportional to the number of people. So that if a third of the pie is one group then that might be 10 out of 30, 12 out of 36. So if you are comparing two pie charts side by side you need to know how many people are being represented.

Students need to see that if

90° represents 8 people

45° represents 4 people

135° represents 12 people

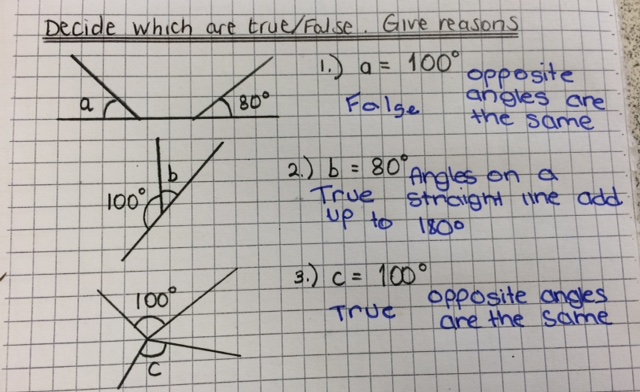
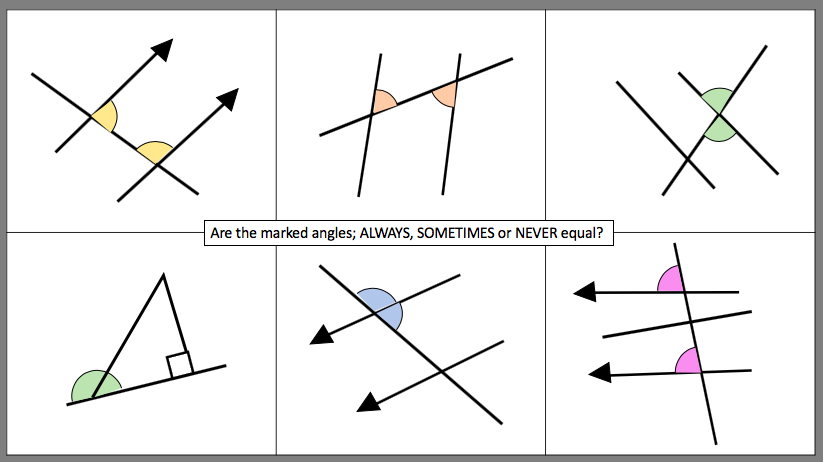
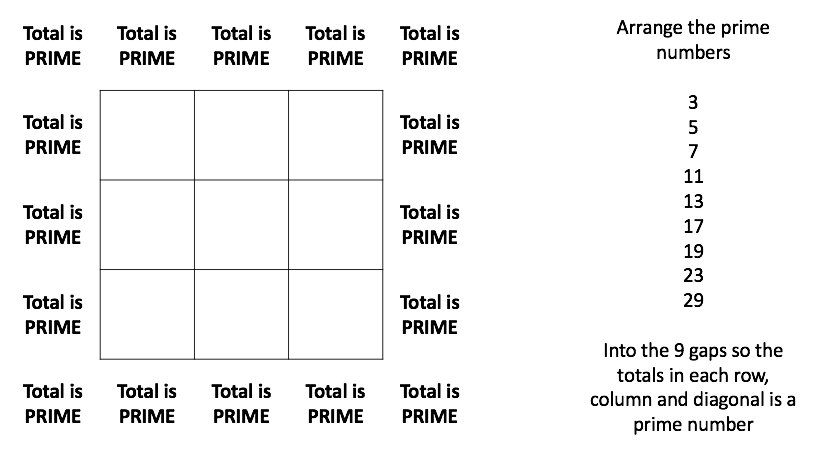
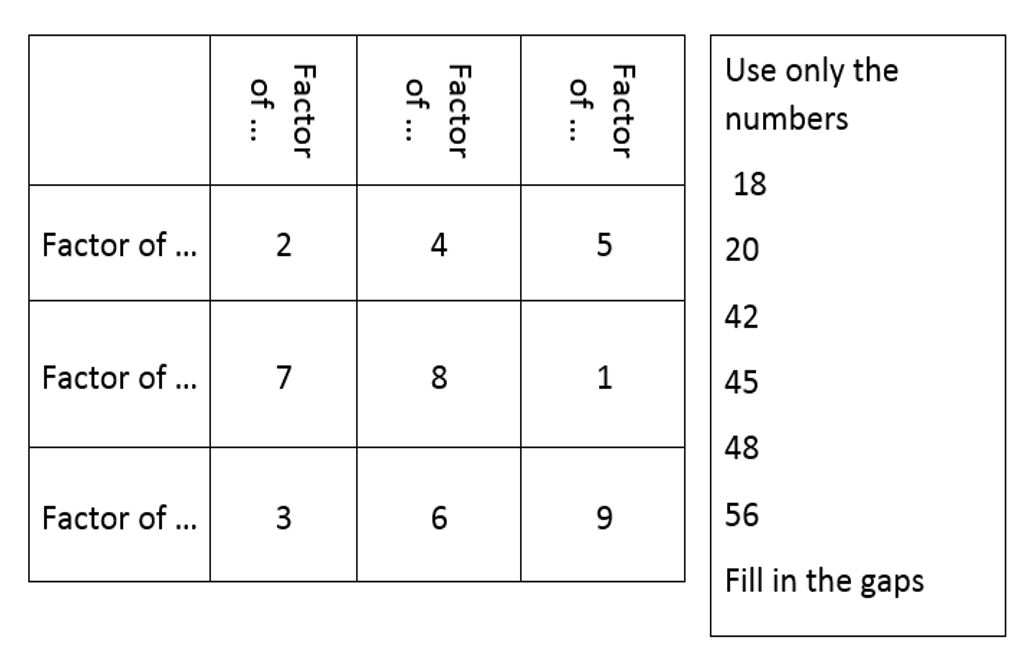
I want to ask questions (TRUE/FALSE) to see what misconceptions students have when understanding Pie Charts. There are lots of much better questions but these are what i have so far. I created this two way table for pie charts and it has two gaps for pie to be created to fit the remaining spaces.

Below are the ppt and worksheet for pie charts

Pie Charts

Pie Charts

Update!

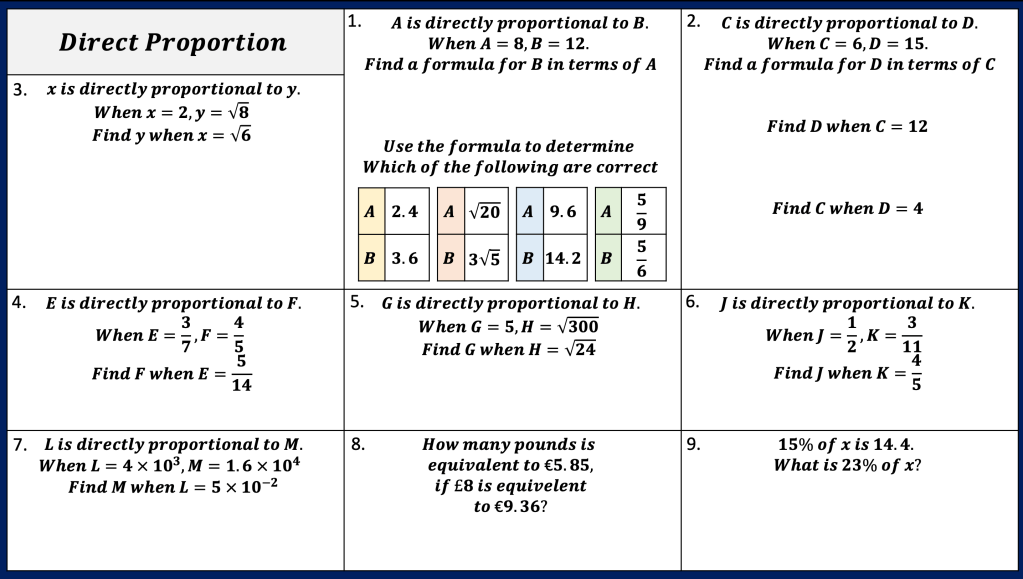
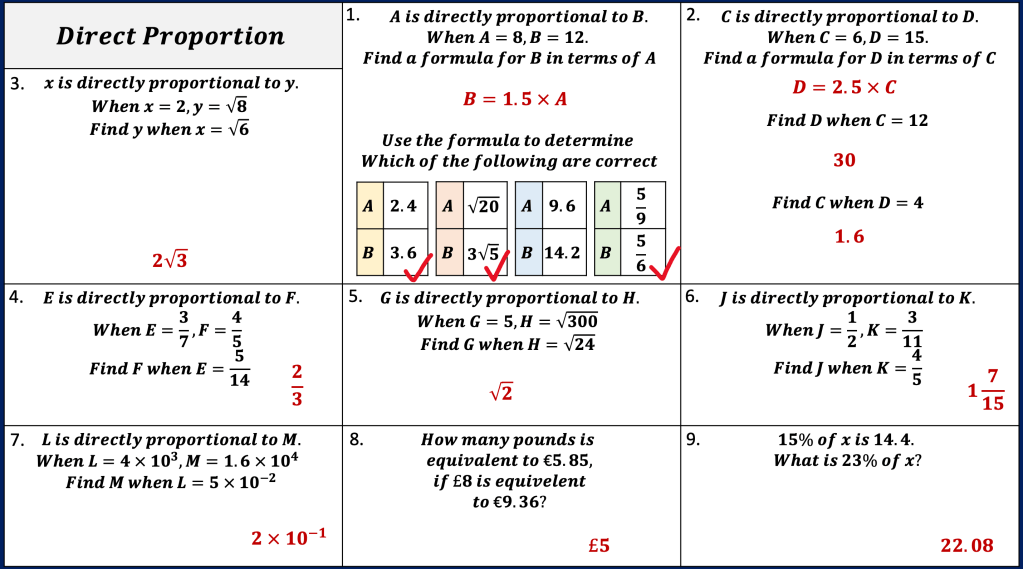
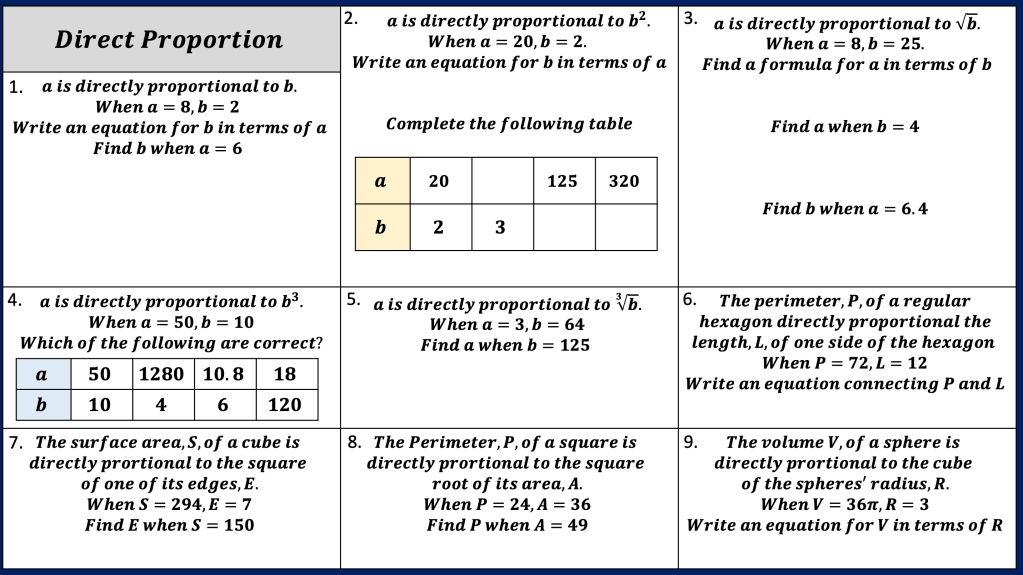
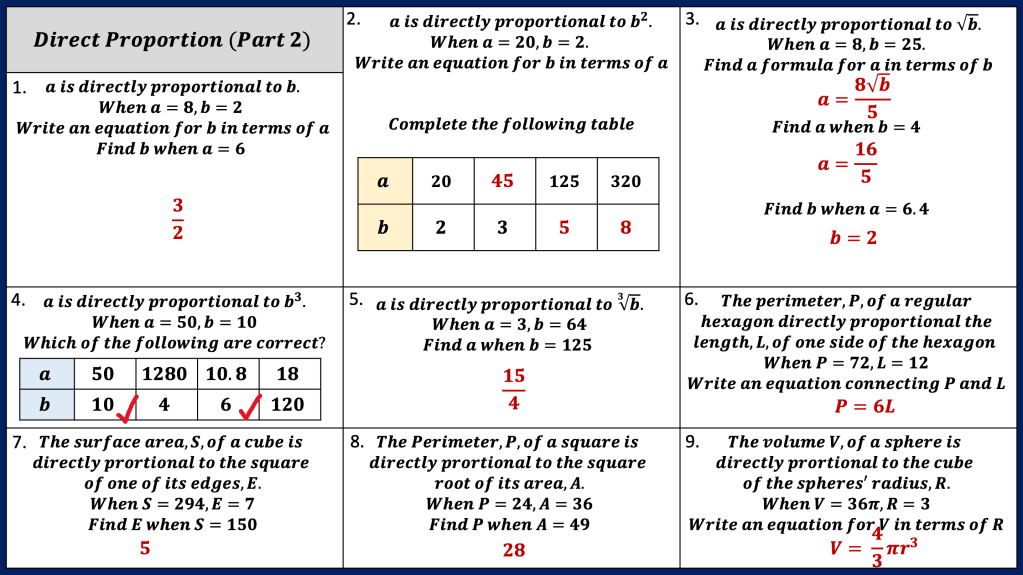
Here is a little pie chart activity i used with my class when i taught proportion

Pie Charts

I have been marking the November GCSE Maths resit and there was a pie chart question on it that candidates really struggled with. With an understanding of proportional reasoning, candidates would be able to answer the question.

Pie Charts

I have been teaching proportional reasoning in my year 11 lessons and then I was given the topics of similarity and congruence for my year 9 class. I am also teaching fractions at Ks3. So I started thinking about how students try to use LCM to find common denominators when adding fractions but when asked if two shapes are similar students usually try to find a scale factor.

I trialled a few questions with year 9 first… the biggest issues were with addition being used that wasn’t rated addition and not understanding that they could look at the scale factor between length/width in the same shape as well as length to length and width to width. If I looked at 3/4.2 and 5/7 I might consider that 3/4.2=30/42=15/21 so they are similar.

Update: After a discussion on Twitter with @petergates3 – he made the comment below. So i rethought the task and came up with something a little different. I am glad i did. In the lesson students were able to make sense of the different ways to check if two shapes are similar. They drew, they discussed and when it came to trying questions they referred to different approaches

I wanted to share a few resources I have made for students who are looking at similar triangles. I the first worksheet I wanted students to realise/note that when two shapes are similar there is a scale factor between all 3 sides from one triangle to another but also there is a connection between the sides. For example; side B is always 3 times the length of A no matter what triangle is drawn (if they are similar)

I also wanted students to notice that you can use all the method they use in ratio to answer these questions. So if they are working from a length of 8cm to a length of 6cm. They can divide the 8cm by 4 then multiply by 3 or multiply by 6 and divide by 8 and so on. This would also work quite well in a pythagoras lesson as a starter. You could remove the right angle and fill in some of the values and ask students to decide whether the triangles were right angled or not and how you can tell.

Here the questions have a repeated length.

Here is the ppt for this lesson with a number starter.

Similarity

similarity-copy.pptx

Some of the difficulties that my year 9 have had with angles during this unit of work

In the Angle reasoning topic I think the focus needs to be on the reasoning and not so much the calculation. You can spend some time asking them to find the 3rd angle of a triangle, but understanding why an angle is 40° show a deeper understanding. I like to get students to draw triangles on dotty paper and then categorize them as isosceles, equilateral etc. This reinforces their understanding of each triangle.

Then i like to give students this task or similar:

Angles

After I gave the following questions which are angles in a triangle but in a shape that has been split into triangles.

Students were encouraged to use highlighters to make parts stand out and to cover up sections so the whole diagram isn’t overwhelming.

Angles in Triangles

Here are some resources on that in the ppt above

Angles on parallel lines

UPDATE:

Here’s a task I created because many of my students made assumptions about lines being parallel and just looked for alternate and corresponding angles in any lines regardless of marked parallel lines. Students can discuss when they might be or never can be and why.

Are they…

There are many ways to introduce and express numbers as a product of prime factors but recently I have been looking at questions that use prime factor form.

I’m not including HCF or LCM in this because most teachers have used PFF to solve HCF and LCM problems before.

Here are some questions I have written that can be solved easily using PFF

These are on the ppt below

Prime Factor Form

I also like this activity I made, its simple practice but saves paper if you display it as a ppt

Primes and Prime Factors

Update

I made this starter to use with year 10

Prime Factor Form Questions

UPDATE! Prime Factor Form Challenge. The idea is students are faced with increasingly more challenging PFF questions. They need to think about divisibility to help them and they know the numbers are listed below. It can generate some interesting discussions about numbers/divisibility. Students who are faced with a large number that isn’t divisible by 2, 3 or 5 may believe the remainder is a prime number. Once the number is written in PFF they can asign the correct letters and unscramble the word.

Here is the ppt for PFF pff

Prime Factor Questions

Prime Factors

I was thinking about the factors particular numbers and considered how many factors int he numbers from 1-40. When I reached the 30s I was surprised how many numbers could be written as a product of two primes, meaning they have 4 factors in total. So I started wondering about what students would make of it. Would they realise if the number was written as a product of two primes it would have 4 factors and would they realise you could easily find a number with 4 factors by multiplying 2 primes together.

33=3×11

34=2×17

35=5×7

38=2×19

39=3×13

The link for the ppt for the puzzles below

Primes

There are so many great resources for students to look at factors and primes. Depending on set and age, I have used many varied problems and questions. Sometimes I start with Squares, Sticks or Rectangles. For this task students take 1 square and they have to arrange it as a square, if this isn’t possible they try a rectangle with length greater than one, if this isn’t possible they draw a stick (one dimension can be 1). So they draw a square for 1, sticks for 2 and 3, then a square for 4, stick for 5, a 3×2 rectangle for 6, a stick for 7 and so on.

Another way I like to start this topic is with this question

Students start discussions of divisibility and more often than not students mention primes. This question is also nice when looking at sequences. Students think about generating a list of possible numbers and it starts conversations about which numbers can be used ‘it will be odd as cant divide 2 exactly’

Once students are familiar with the terms ‘factors’ and ‘prime’ I like to move one to some problems where it tests their abilities to determine whether a number is a prime or what factors it has.

I usually use the above task as a plenary task which you’ll find on the ppt below and I sometimes restrict the numbers and other times allow them to use any number.

Types of Number

Types of Number

The two task above are from the worksheet below and students have to think about factors of numbers but it also introduces HCF and finding common factors of two numbers.

Factor 2 Way Tables

I usually finish with a task like below and although you get the students picking out 20 because its the only EVEN you do get students using ‘factor of’ and ‘not a prime’

It leads to some interesting discussions.

This proved an interesting starter. Some students filled it in then realised it didnt add up to 15!

Updated for Christmas!

A simple dot to dot snowflake for students to do as a starter

Types of Number Dot to Dot

Similar Shapes

On the back of using this resource below with my year 10 low attaining class I realised they struggled with more than one rule/statement. So I created some more practice of simpler Loci problems

loci

Loci Starter and Problem

After a few lessons looking at different ruler and compass constructions, we looked at the following activity;

Loci activity

Students were to identify all the points exactly 3cm from A in the first diagram

In the second diagram they had to identify points equidistant from AB and AC

In the third diagram they had to identify points equidistant from A and B

In the fourth diagram they had to identify points 2cm from the line AB

In the fifth diagram they had to identify points exactly 1cm from the shape A

I saw lots of students, ruler in hand measuring the points, some drew lines, like radii in the first problem and i asked them what they would do if i had drawn loads of points on the page, say 100. A few students noticed the circular shape to  the points identified and i think if i had drawn loads more points this might have been a little clearer to the students. This activity did help students when they had no idea of what the loci of points might look like. Later in the lesson students were seen locating points to help them see what shape the loci was creating.

Loci

I set the following problem in the lesson on Loci

Loci Problem

I made an overlay on tracing paper with the solution so i could check answers (completed or not) This task wasn’t just about Loci but also area and you can solve it without constructing anything. Students constructed the 4 maps to locate the treasure but didn’t answer the question!

update!

This year I went back to this resource and amended it.

We spent time trying to place objects so they followed a rule then discussed what we noticed.

Just recently i showed my students the angle bisector and perpendicular bisector constructions and we discussed why they worked. I allowed them some time to attempt the constructions themselves and as i walked around to help students with using the equipment i noticed a lot of mistakes. I recreated these mistakes and have put them into a ppt so that the class can discuss what is wrong about each construction.

Most of the mistakes made in the constructions were quite easy to spot but the one below right was harder. They eventually saw it was the two arcs that were constructed from the incorrect place that made the bisect wrong.

Construction

After looking at these errors i gave the students the following questions

The idea with these questions was to get students to think first about what letter they thought the bisector would pass through before they attempted the construction. This was because many of the students didn’t pay attention to whether their answer was sensible. I saw constructions where it was very obvious to the naked eye that the bisector wasn’t where they drew it. It also made it easy to get a rough idea of if the class could get the construction right by the simple fact the line should go through B. Obviously this doesn’t mean they definitely got it right but it was a start.

At the end of the lesson I gave the class the challenge of trying to construct a 45° angle

I let the students discuss it in pairs and i gave them a clue that you could do it with two constructions. With help they were able to arrive at the idea of bisecting the angle on a perpendicular bisector.

Constructing Triangles

I would like to discuss what errors are made her with my students…

Students often forget to draw in the angle bisector after constructing the arcs or ignore the first arc or make the arcs too short. I’m hoping these will help them avoid those errors.

I used a little activity with my year 8 that i thought of whilst teaching them. They were looking at Bounds and we were discussing which numbers equal 5 when rounded to the nearest whole number. They could list 4.5, 4.6, 4.7, 4.8, 4.9, 5.1, 5.2, 5.3, 5.4 but didn’t pick up on 5 itself or all the other numbers from 4.5 and up to but not including 5.5. So i told them i was thinking of a number they could ask me a question like; ‘What is your number rounded to the nearest 10’ or something similar and when they thought they had my number they could guess it.

My first number was 512.

They asked ‘What is your number rounded to the nearest 100?’. I said 500

Next they asked; ‘What is your number rounded to the nearest 10?. I said 510

Next they asked; ‘What is your number rounded to the nearest whole number?. I said 512.

Then a student guessed 512. 

Next i chose the number 430.6991

Feeling a little smarter they asked ‘What is your number rounded to the nearest 1 decimal place?’. I said 430.7

Next they asked; ‘What is your number rounded to the nearest 2 decimal places?. I said 430.70

Then a student guessed 430.7

I said no. They were very confused at this point. After a while a student said  ‘What is your number rounded to the nearest 3 decimal places?. I said 430.699

Then a student guessed 430.699

My next number was going to be 400.0005 but we ran out of time!

 

I like these little tricks and students seem to enjoy them too, I usually start with a simple one like: I think of a number, add 3, double it, subtract 6 and halve it. If they quickly work out that my answer will always get back to my start number, we then look at why. We look at writing the calculations out without calculating but just simplifying if possible

So if they used 4…

4 ( i think of a number)

4+3 (add 3)

4+4+3+3 (double it)

4+4+3+3-6 = 4+4 (subtract 6)

4 (Halve it)

When you compare each student they can see the variables and the constants. They can start to generalise. The student work below is an example of using values and then generalising. I asked how he got from add 6 to halve it and he said that 7 x 2 + 6 is 7 + 3 because you only have one 7 when you have 7 x 2 and half of 6 is 3. After working through these a few students asked if they could try and make their own up. So next lesson we hope to try and write some expressions and put words to them. The students noticed how my tricks always came back to the original number or a specific number and they want to try and make their own versions of these.

I think of a number

I was thinking that next lesson

What i hope is for them to write the words to my expressions and then get them to work using numbers or letters if they prefer to create a series of slightly altered expressions of their own.

I want to display the slide above and ask them to explain what they notice to be the same and what changes. What they notice has to apply to all 3 examples. They could write out an example of their own if it helps.

Solving Equations

 I_think_of_a_number[1]

Solving_Equations[1]

After spending several lessons looking at inverse and direct proportion i decided my students needed a chance to try a mix of both inverse and direct proportion questions. They are very basic but the students get a chance to determine which approach to use as well as applying the method.

Proportion

I used the starter above to get past issues with solving equations and using a calculator.

Then i set the following sheet

I put the answers up so students could tell me (which they did) if there was a question they got an answer that didn’t appear on the screen. The colours represented direct or inverse.